波门

发表于 2020-07-17 更新于 2021-05-08 分类于 Tracking

目标跟踪中波门形状与参数

环形波门

环形波门一般用于航迹起始的初始化，是半径为$V_{min}\times T$和$V_{max}\times T$的圆包围的圆环

椭圆（球）波门

若传感器测得的目标直角坐标系下的转换量测值 $Z_{c}(k+1)$ 满足:

$\begin{aligned} \tilde{V}_{k+1}(\gamma) \underline{\Delta} &\left[\boldsymbol{Z}_{c}(k+1)-\hat{\boldsymbol{Z}}_{c}(k+1 \mid k)\right]^{\prime} \boldsymbol{S}^{-1}(k+1)\left[\boldsymbol{Z}_{c}(k+1)-\hat{\boldsymbol{Z}}_{c}(k+1 \mid k)\right] \\ &=\boldsymbol{v}_{c}^{\prime}(k+1) \boldsymbol{S}^{-1}(k+1) \boldsymbol{v}_{c}(k+1) \leqslant \gamma \end{aligned}$

则称转换量测值 $\boldsymbol{Z}_{c}(k+1)$ 为候选回波，上式称为椭圆（球）波门规则。其中参数由 $\chi^{2}$ 分布表获得。若量测值 $\boldsymbol{Z}_{c}(k+1)$ 为 $n_{z}$ 维，则 $\tilde{\boldsymbol{V}}_{k+1}(\gamma)$ 是将残差标准化后的具有 $n_{z}$ 个自由度的 $\chi^{2}$ 分布随机变量。

$\gamma$的值可以通过matlab函数chi2inv(1-alpha,nz)生成

对于不同 $\gamma$ 值和不同量测维数 $n_{z},$ 真实转换量测落入波门内的概率 $P_{\mathrm{G}}$ 就不同，定义

$P_{\mathrm{G}}=\operatorname{Pr}\left\{\boldsymbol{Z}_{c}(k+1) \in \tilde{V}_{k+1}(\gamma)\right\}$

$P_{\mathrm{G}}$ 与量测维数 $n_{z}$ 和参数 $\gamma$ 的关系式可用下表表示。

相应的$P_G$计算的matlab代码如下：

function P_G = PG(gamma,N_z)
% 只实现了4维
    switch (N_z)
        case 1
            P_G = 2*(normcdf(sqrt(gamma)) - normcdf(0));
        case 2
            P_G = 1-exp(-gamma/2);
        case 3
            P_G = 2*(normcdf(sqrt(gamma)) - normcdf(0)) - sqrt(2*gamma/pi)*exp(-gamma/2);
        case 4
            P_G = 1-(1+gamma/2)*exp(-gamma/2);
        otherwise
    end
end

$n_{z}$ 维析圆（球）波门的面（体）积为

$V_{\text {椭}}\left(n_{z}\right)=c_{n_{z}} \gamma^{\frac{n_{z}}{2}}|\boldsymbol{S}(k+1)|^{\frac{1}{2}}$

式中

$c_{n_{z}}=\left\{\begin{array}{cc} \frac{\pi^{\frac{n_{z}}{2}}}{\left(n_{z} / 2\right) !}, & n_{z} \text { 为偶数 } \\ \frac{2^{n_{z}+1}\left(\frac{n_{z}+1}{2}\right) ! \pi^{\frac{n_{z}-1}{2}}}{\left(n_{z}+1\right) !}, & n_{z} \text { 为奇数 } \end{array}\right.$

当 $n_{z}=1,2,3$ 时， $c_{n_{z}}$ 分别为 $2, \pi$ 和 $4 \pi / 3$。

利用新息协方差的标准差归一化可以得到

$V^{u}_{\text {椭}}\left(n_{z}\right)=c_{n_{z}} \gamma^{\frac{n_{z}}{2}}$

通过下式进行归一化：

$\frac{\boldsymbol{Z}_{c}(k+1)-\hat{\boldsymbol{Z}}_{c}(k+1 \mid k)}{\sqrt{\mid\mathbf{S(k+1)}\mid}}$

相应的$V_{\text {椭}}\left(n_{z}\right)$计算的matlab代码如下：

function [Volume] = ellipse_Volume(gamma,N_z,S)
    switch (N_z)
        case 1
            Volume = 2*sqrt(gamma)*sqrt(det(S));
        case 2
            Volume = pi*gamma*sqrt(det(S));
        case 3
            Volume = 4*pi/3*gamma^(3/2)*sqrt(det(S));
        otherwise
    end
end

航迹起始

发表于 2020-07-15 更新于 2021-05-08 分类于 Tracking

MN逻辑法航迹起始

设 $z_{i}^{l}(k)$ 是 $k$ 时刻量测 $i$ 的第 $l$ 个分量，这里 $l=1, \cdots, p, \quad i=1, \cdots, m_{k}, \quad$ 则可将观测值
$\boldsymbol{Z}_{i}(k)$ 与 $\boldsymbol{Z}_{j}(k+1)$ 间的距离矢量 $\boldsymbol{d}_{i j}$ 的第 $l$ 个分量定义为

$d_{i j}^{l}(t)=\max \left[0, z_{j}^{l}(k+1)-z_{i}^{l}(k)-v_{\max }^{l} T\right]+\max \left[0,-z_{j}^{l}(k+1)+z_{i}^{\prime}(k)+v_{\min }^{l} T\right]$

式中， $T$ 为两次扫描问的时间问隔。若假设观测误差是独立、零均值、高斯分布的，方差为 $\boldsymbol{R}_{i}(k), \quad$ 则归一化距离平方为

$D_{i j}(k) \triangleq \boldsymbol{d}_{i j}^{\prime}\left[\boldsymbol{R}_{i}(k)+\boldsymbol{R}_{j}(k+1)\right]^{-1} \boldsymbol{d}_{i j}$

式中， $D_{i j}(k)$ 为服从自由度为 $p$ 的 $\chi^{2}$ 分布的随机变量。由给定的门限概率查自由度 $p$ 为 $\chi^{2}$ 分布武可得门限 $\gamma, \quad$ 若 $D_{i j}(k) \leqslant \gamma,$ 则可判定 $Z_{i}(k)$ 和 $\boldsymbol{Z}_{\boldsymbol{j}}(k+1)$ 两个量测互联。

仿真代码

首先为了方便后续代码管理定义航迹的类

classdef Track
    properties
        start = [];
        seq = [];
        est  = [];
        pkk = [];
        x_predict = [];
    end
    methods
        function obj = Track(Z)
            obj.start = Z;
            obj.seq   = Z;
        end
        function show(obj)
            plot(obj.est(1,:),obj.est(2,:),'linewidth',2);
        end
    end
end

接下来就是实现航迹起始的函数:
采用线性贝叶斯迭代方法进行外推与波门大小的估计
航迹起始采用逻辑法的判别
后续的外推判决采用最邻近滤波(NN)方法

function [Root] = MNStarter(points,N,M,vmin,vmax)
% points 是为N次量测的集合
% N 如上
% M 航迹确认的门限
% vmin 速度最小值 用于初始化的圆（球）波门
% vmax 速度最大值 用于初始化的圆（球）波门

% Root 返回值为Track类的变量

T = 1;

threshold = chi2inv(0.8,2);

track = {};

F = [1 0 T 0;
     0 1 0 T;
     0 0 1 0;
     0 0 0 1];
H = [1 0 0 0;
     0 1 0 0];
Gamma=[T*T/2 0;0 T*T/2;T 0;0 T];
Q = Gamma*Gamma'*0.1;%根据实际过程噪声的协方差更改
R = 5*H*H';  %根据实际测量误差的协方差更改
pair = {};  

outside = [];
set = [];
index = 1;

Z_k = cell2mat(points(1));
Z_k_plus1 = cell2mat(points(2));
for j = 1:size(cell2mat(points(1)),2)    
    for k = 1:size(cell2mat(points(2)),2)    
       d = max(0,norm(Z_k_plus1(:,k)-Z_k(:,j))-vmax*T)+max(0,-norm(Z_k_plus1(:,k)-Z_k(:,j))+vmin*T);
       D = d'*(R+R)^-1*d;
       if D <= threshold
            pair = [pair ;[Z_k(:,j),Z_k_plus1(:,k)]];
            
            % 初始化协方差
            Px0 = 5*eye(4);
            P=F*Px0*F'+Q;%预测协方差阵
            S(:,:,index)=H*P*H'+R;%计算新息协方差
            K = P*H'*inv(S(:,:,index));
            Pkk(:,:,index) = (eye(4)-K*H)*P;%计算后验方差
            
            %计算由前两次量测组成的直线进行外推
            x_init=[Z_k_plus1(:,k);(Z_k_plus1(:,k)-Z_k(:,j))/T];%利用前两个观测值来对初始条件进行估计
            
            x_forest(:,index)=F*x_init;%状态的一步预测
            out_forest=H*x_forest(:,index);%观测的一步预测
            outside=[outside out_forest];%外推点
            
            index = index +1;
       end
    end
end

board = zeros(1,size(pair,1)); %计分板

for j=3:N
    Z_k = cell2mat(points(j));
    for t=1:index-1 
        P=F*Pkk(:,:,t)*F'+Q;
        SS = H*P*H' + R;
        K = P*H'*inv(SS);
        for i=1:(size(Z_k,2))
            %计算后续的扫描点落在外推点跟踪门内的系数
            V(i)=(Z_k(:,i)-outside(:,t))'*inv(SS)*(Z_k(:,i)-outside(:,t));
        end
        [key dex]=min(V);
        %判断是否有回波落入到门波之内，有则取离外推点最近的给予互联
        if (key<=threshold)
%             x_init=[Z_k(:,dex);(Z_k(:,dex)-pair{t}(:,end))/T];
%             pair(t,:)={[pair{t} Z_k(:,dex)]};
%             x_forest=F*x_init;
%             outside(:,t)=H*x_forest;
            pair(t,:)={[pair{t} Z_k(:,dex)]};
            x_est = x_forest(:,t) + K*(Z_k(:,dex)-outside(:,t));
            Pkk(:,:,t) = (eye(4)-K*H)*P;
            x_forest(:,t)=F*x_est;
            outside(:,t)=H*x_forest(:,t);
        else
            pair(t,:)={[pair{t} outside(:,t)]};
            
            Pkk(:,:,t) = P;
            x_forest(:,t)=F*x_forest(:,t);
            outside(:,t)=H*x_forest(:,t);
            board(t) = board(t)+1;
        end       
    end
    V=[];
end

% icon=['*','+','o','s','d','.'];
% figure
% hold on
% for i = 1:N
%     Z = cell2mat(points(i));
%     plot(Z(1,:),Z(2,:),icon(mod(i,6)+1));
% end

num_trace = 0 ; 
index = 1;
for i = 1:size(pair,1)
    trace = cell2mat(pair(i));
    if N-board(i) >= M
%         plot(trace(1,:),trace(2,:),'pk');
%         plot(trace(1,:),trace(2,:),'-');
%         pause(0.5);
        Root(index) = Track(trace(:,1));
        Root(index).seq = trace;
        index = index +1;
        num_trace = num_trace + 1;
    end
end


for i = 1:num_trace
    xe = [];
    xe(:,1) =[ Root(i).start;zeros(2,1)];
    P = eye(4);
    for j = 2:size(Root(i).seq,2) 
        [xe(:,j),P] = KalmanFilter(Root(i).seq(:,j),xe(:,j-1),F,H,P,Q,R);
    end
    Root(i).pkk = P;
    Root(i).est = xe;
    Root(i).x_predict = F*xe(:,j);
    
%     plot(xe(1,:),xe(2,:),'linewidth',2);
end

% figure
% hold on
% for i = 1:num_trace
%     Root(i).show;
% end

end

接下来给出一个测试的代码:

clc;close all;clear all
load('points_prev.mat');

N = 8;
M = N * 3 /4;

vmin = 0.5;
vmax = 4;

[Root] = MNStarter(points,N,M,vmin,vmax);

figure
hold on
for i = 1:size(Root,2)
    Root(i).show;
end
xlabel('x轴坐标(m)');
ylabel('y轴坐标(m)');
title('mn逻辑法航迹起始');

运行可以得到:

如果多个目标距离较远,并且虚警率较低那么通过NN方法就可以经进行航迹的绘制
将上面的测试代码N更改为40

基于RLS的脉压雷达数字旁瓣抑制滤波器设计

发表于 2020-07-09 更新于 2021-05-08 分类于 Radar Signal Processing

原理简述

采用自适应滤波器设计中的递归最小二乘(RLS)方法，通过合理安排输入信号与期望信号的结构来设计脉冲压缩雷达数字旁瓣抑制滤波器，具有算法简单实用，适用广泛的特点，可用于线性调频、二相码和多相码等各种信号。在滤波器抽头有限的情况下，峰值旁瓣电平低于-40dB。主瓣宽度仅为单位采样符号间隔。

衡量旁瓣抑制滤波器性能的指标主要有峰值旁瓣电平(PSL，peak side lobe level)和积累旁瓣电平(ISL，integrated side lobe level)，它们分别定义为最大旁瓣功率与峰值响应的比值以及旁瓣总功率与峰值响应的比值。

对于雷达来说，理想的匹配滤波压缩波形应为一$\delta$函数。在实际的脉压波形中，非零旁瓣可视为噪声，于是，旁瓣抑制过程可看作是自适应噪声对消，只不过输入为原始的压缩信号(匹配滤波输出)。下图表示出了在迭代训练时，这种横向滤波器的结构框图。

若设$\boldsymbol{x}$为$f_s(t)$的匹配滤波输出包络 , 则迭代时,输入信号$\boldsymbol{u}$应为$\boldsymbol{x}$的重复。为了消除前后$\boldsymbol{x}$之间的影响 ,其间应插入零向量$\boldsymbol{z}$, 且$\boldsymbol{z}$的长度应至少为所设定的滤波器长度。这样才能使信号$\boldsymbol{x}$全部移出滤波器后 ,下一个$\boldsymbol{x}$才进入滤波器;同时为了减少迭代次数, 零向量的长度又不宜过长。故$\boldsymbol{u}$为

$\boldsymbol{u} = [\boldsymbol{x} \ \boldsymbol{z} \ \boldsymbol{x} \ \boldsymbol{z} \dotsb]$

且有关系

$L_w =L_z$

式中, $L_w$为滤波器抽头长度;$L_z$为零向量 z的长度。

期望响应$\boldsymbol{d}$为理想狄拉克信号$\delta$的周期重复

$\boldsymbol{d} = [\delta \ \delta \ \delta \dotsb]$

考虑到FIR滤波器的时延特性那么，在$\delta$中，1的位置在$(L_w+L_x)/{2}$。

之后根据RLS迭代算法

$\left\{\begin{array}{l} e(n)=d(n)-\boldsymbol{w}^{H}(n-1) \boldsymbol{u}(n) \\ \boldsymbol{k}(n)=\frac{\boldsymbol{P}(n-1) \boldsymbol{u}(n)}{\lambda+\boldsymbol{u}^{H}(n) \boldsymbol{P}(n-1) \boldsymbol{u}(n)} \\ \boldsymbol{P}(n)=\frac{1}{\lambda}\left[\boldsymbol{P}(n-1)-\boldsymbol{k}(n) \boldsymbol{u}^{H}(n) \boldsymbol{P}(n-1)\right] \\ \boldsymbol{w}(n)=\boldsymbol{w}(n-1)+\boldsymbol{k}(n) e^{*}(n) \end{array}\right.$

初始化条件：

$\begin{array}{l} \boldsymbol{w}(0)=\boldsymbol{0} \\ \boldsymbol{P}(0)=\rho^{-1} \boldsymbol{I} \end{array}$

其中$\rho$为正则化参数,其设定与信噪有关, 高信噪比时取较小值,低信噪比时取较大值。

仿真结果

13位Barker码二进制相位调制波形仿真

13位巴克码码元为$[1,1 ,1, 1, 1, -1 ,-1 ,1 ,1 ,-1 ,1 ,-1, 1 ]$

通过匹配滤波器的结果如图

经过RS-RLS自适应滤波设计滤波器系数后得到

通过对不同长度的滤波器进行PSL和ISL指标进行仿真得到

LFM信号仿真

通过匹配滤波器的结果如图

经过RS-RLS自适应滤波设计滤波器系数后得到

通过对不同长度的滤波器进行PSL和ISL指标进行仿真得到

概率最邻近数据关联算法

发表于 2020-07-09 更新于 2021-05-08 分类于 Tracking

$\begin{array}{c} \hat{\boldsymbol{X}}(k \mid k)=\hat{\boldsymbol{X}}(k \mid k-1) \\ \boldsymbol{P}(k \mid k)=\boldsymbol{P}(k \mid k-1)_{M_{0}}=\boldsymbol{P}(k \mid k-1)+\frac{P_{\mathrm{D}} P_{\mathrm{G}}\left(1-C_{\tau g}\right)}{1-P_{\mathrm{D}} P_{\mathrm{G}}} \boldsymbol{K}(k) \boldsymbol{S}(k) \boldsymbol{K}^{\prime}(k) \end{array}$

IMMKF

发表于 2020-07-01 更新于 2021-05-08 分类于 Tracking

交互多模型

滤波模型

假定目标动态特性包含在以下模型集中：

$\boldsymbol{x}_{k}=\boldsymbol{f}_{r_{k}}\left(\boldsymbol{x}_{k-1}, \boldsymbol{u}_{k}\right)+\boldsymbol{v}_{r_{k}}, \quad r_{k} \in\{1,2, \cdots, d\}$

$r_{k}$ 是在状态空间内 $\{1,2, \cdots, d\}$ 满足一致性离散马尔可夫链的随机变量。

目标状态的后验概率密度 $p\left(\boldsymbol{x}_{k} \mid \boldsymbol{y}^{k}\right)$ 通过对联合概率密度各分量求和得

$p\left(\boldsymbol{x}_{k} \mid \boldsymbol{y}^{k}\right)=\sum_{i=1}^{d} p\left(\boldsymbol{x}_{k}, r_{k}=i \mid \boldsymbol{y}^{k}\right)$

利用条件概率引理，上述方程右侧的联合概率密度可以分解为两项之积，即

$p\left(\boldsymbol{x}_{k}, r_{k}=i \mid \boldsymbol{y}^{k}\right)=p\left(\boldsymbol{x}_{k} \mid r_{k}=i, \boldsymbol{y}^{k}\right) p\left(r_{k}=i \mid \boldsymbol{y}^{k}\right)$

令 $\mu_{k \mid k}(i)=p\left(r_{k}=i \mid \boldsymbol{y}^{k}\right),$ 后验概率密度可以表示为

$p\left(\boldsymbol{x}_{k} \mid \boldsymbol{y}^{k}\right)=\sum_{i=1}^{d} p\left(\boldsymbol{x}_{k} \mid r_{k}=i, \boldsymbol{y}^{k}\right) \mu_{k \mid k}(i)$

将 $\boldsymbol{y}^{k}$ 展开为 $\left\{\boldsymbol{y}_{k}, \boldsymbol{y}^{k-1}\right\}$,利用贝叶斯理论可以得到上述方程右侧求和第一项的递推式:

$\begin{aligned} p\left(\boldsymbol{x}_{k} \mid r_{k}=i, \boldsymbol{y}^{k}\right) &=p\left(\boldsymbol{x}_{k} \mid r_{k}=i, \boldsymbol{y}_{k}, \boldsymbol{y}^{k-1}\right) \\ &=\frac{p\left(\boldsymbol{y}_{k} \mid \boldsymbol{x}_{k}, r_{k}=i, \boldsymbol{y}^{k-1}\right)}{p\left(\boldsymbol{y}_{k} \mid r_{k}=i, \boldsymbol{y}^{k-1}\right)} p\left(\boldsymbol{x}_{k} \mid r_{k}=i, \boldsymbol{y}^{k-1}\right) \end{aligned}$

式中: $p\left(\boldsymbol{x}_{k} \mid r_{k}=i, \boldsymbol{y}^{k-1}\right)$ 为预测概率密度 $; p\left(\boldsymbol{y}_{k} \mid \boldsymbol{x}_{k}, r_{k}=i, \boldsymbol{y}^{k-1}\right)$ 为似然函数 ; $p(\boldsymbol{y}_{k} \mid r_{k}=i, \boldsymbol{y}^{k-1}$ ) 为归一化因子。式(3.45)的求和分量第二项 $\mu_{k \mid k}(i)=p\left(r_{k}=i \mid \boldsymbol{y}^{k}\right)$ 也可以通过递推计算。同样将 $\boldsymbol{y}^{k}$ 展开为 $\left\{\boldsymbol{y}_{k}, \boldsymbol{y}^{k-1}\right\},$ 利用贝叶斯理论可得

$\begin{aligned} \mu_{k \mid k}(i)=p\left(r_{k}=i \mid \boldsymbol{y}_{k}, \boldsymbol{y}^{k-1}\right)=\frac{p\left(\boldsymbol{y}_{k} \mid r_{k}=i, \boldsymbol{y}^{k-1}\right) p\left(r_{k}=i \mid \boldsymbol{y}^{k-1}\right)}{p\left(\boldsymbol{y}_{k} \mid \boldsymbol{y}^{k-1}\right)} \end{aligned}$

令 $p\left(r_{k}=i \mid \mathbf{y}^{k-1}\right)=\boldsymbol{\mu}_{k \mid k-1}(i),$ 条件模型概率可表示为

$\begin{aligned} \mu_{k \mid k}(i)=\frac{p\left(\boldsymbol{y}_{k} \mid r_{k}=i, \boldsymbol{y}^{k-1}\right) \mu_{k \mid k-1}(i)}{p\left(\boldsymbol{y}_{k} \mid \boldsymbol{y}^{k-1}\right)} \end{aligned}$

式中: $\mu_{k \mid k-1}(i)$ 为模型预测概率 $; p\left(\boldsymbol{y}_{k} \mid r_{k}=i, \boldsymbol{y}^{k-1}\right)$ 为似然函数 $; p\left(\boldsymbol{y}_{k} \mid \boldsymbol{y}^{k-1}\right)$ 为归一
化因子。

某一模型的状态的预测概率密度和预测的模型概率

$\begin{aligned} p\left(\boldsymbol{x}_{k} \mid r_{k}=i, \boldsymbol{y}^{k-1}\right) &=\int_{\boldsymbol{x}_{k-1}} p\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{k-1}, r_{k}=i, \boldsymbol{y}^{k-1}\right) \sum_{j=1}^{d} p\left(\boldsymbol{x}_{k-1} \mid r_{k-1}\right.\\ &\left.=j, \boldsymbol{y}^{k-1}\right) \mu_{k-11 k}^{j i} \mathrm{d} \boldsymbol{x}_{k-1} \\ &=\int_{\boldsymbol{x}_{k-1}} N\left(\boldsymbol{x}_{k} ; \boldsymbol{F}_{i} \boldsymbol{x}_{k-1}+\boldsymbol{u}_{i}, \boldsymbol{Q}_{i}\right) N\left(\boldsymbol{x}_{k-1} ; \hat{\boldsymbol{x}}_{k-1 \mid k-1}^{0 i}, \boldsymbol{P}_{k-1 \mid k-1}^{0 i}\right) \mathrm{d} \boldsymbol{x}_{k-1} \\ &=N\left(\boldsymbol{x}_{k} ; \hat{\boldsymbol{x}}_{k \mid k-1}^{i}, \boldsymbol{P}_{k \mid k-1}^{i}\right) \end{aligned}$

其中，均值和协方差分别为

$\begin{aligned} \hat{\boldsymbol{x}}_{k \mid k-1}^{i} =\boldsymbol{F}_{\boldsymbol{i}} \hat{\boldsymbol{x}}_{k-1 \mid k-1}^{0 i}+\boldsymbol{u}_{i} \\ \boldsymbol{P}_{k \mid k-1}^{i}= \boldsymbol{F}_{i} \boldsymbol{P}_{k-1 \mid k-1}^{0 i} \boldsymbol{F}_{i}^{\mathrm{T}}+\boldsymbol{Q}_{i} \end{aligned}$

预测模型概率 $\mu_{k \mid k-1}(i)$ 可以展开为

$\begin{aligned} \mu_{k \mid k-1}(i) &=p\left(r_{k}=i \mid \boldsymbol{y}^{k-1}\right) \\ &=\sum_{j=1}^{d} p\left(r_{k}=i \mid r_{k-1}=j, \boldsymbol{y}^{k-1}\right) p\left(r_{k-1}=j \mid \boldsymbol{y}^{k-1}\right) \\ &=\sum_{j=1}^{d} \Gamma_{j i} p\left(r_{k-1}=j \mid \boldsymbol{y}^{k-1}\right) \\ &=\sum_{j=1}^{d} \Gamma_{j i} \mu_{k-1 \mid k-1}(j) \end{aligned}$

似然函数

$p\left(\boldsymbol{y}_{k} \mid \boldsymbol{x}_{k}, r_{k}=i, \boldsymbol{y}^{k-1}\right)=p\left(\boldsymbol{y}_{k} \mid \boldsymbol{x}_{k}\right)=N\left(\boldsymbol{y}_{k} ; \boldsymbol{H} \boldsymbol{x}_{k}, \boldsymbol{R}_{k}\right)$

令$\lambda_{k}(i)=p\left(\boldsymbol{y}_{k} \mid r_{k}=i, \boldsymbol{y}^{k-1}\right)$则 $\lambda_{k}(i)=N\left(\boldsymbol{y}_{k} ; \boldsymbol{H} \hat{\boldsymbol{x}}_{k-1 \mid k-1}^{i}, \boldsymbol{H} \boldsymbol{P}_{k \mid k-1}^{i} \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{R}_{k}\right)$

归一化因数

$\begin{aligned} p\left(\boldsymbol{y}_{k} \mid \boldsymbol{y}^{k-1}\right) &=\sum_{i=1}^{d} p\left(\boldsymbol{y}_{k} \mid r_{k}=i, \boldsymbol{y}^{k-1}\right) p\left(r_{k}=i \mid \boldsymbol{y}^{k-1}\right) \\ &=\sum_{i=1}^{d} \lambda_{k}(i) \sum_{j=1}^{d} \Gamma_{j i} \mu_{k-1 \mid k-1}(j) \end{aligned}$

条件概率密度和条件模型概率

条件概率密度展开为

$\begin{aligned} p\left(\boldsymbol{x}_{k} \mid r_{k}=i, \boldsymbol{y}^{k}\right) &=\frac{p\left(\boldsymbol{y}_{k} \mid \boldsymbol{x}_{k}, r_{k}=i, \boldsymbol{y}^{k-1}\right) p\left(\boldsymbol{x}_{k} \mid r_{k}=i, \mathbf{y}^{k-1}\right)}{p\left(\boldsymbol{y}_{k} \mid r_{k}=i, \mathbf{y}^{k-1}\right)} \\ &=\frac{N\left(\boldsymbol{y}_{k} ; \boldsymbol{H} \boldsymbol{x}_{k}, \boldsymbol{R}_{k}\right) N\left(\boldsymbol{x}_{k} ; \hat{\boldsymbol{x}}_{k \mid k-1}^{i}, \boldsymbol{P}_{k \mid k-1}^{i}\right)}{N\left(\boldsymbol{y}_{k} ; \boldsymbol{H} \hat{\boldsymbol{x}}_{k \mid k-1}^{i}, \boldsymbol{H} \boldsymbol{P}_{k \mid k-1}^{i} \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{R}_{k}\right)} \end{aligned}$

条件概率密度可以近似为高斯分布, 即 $p\left(\boldsymbol{x}_{k} \mid r_{k}=i, \boldsymbol{y}^{k}\right)=N\left(\boldsymbol{x}_{k} ; \hat{\boldsymbol{x}}_{k \mid k}^{i}, \boldsymbol{P}_{k \mid k}^{i}\right),$ 其
均值和协方差为

$\begin{aligned} \hat{\boldsymbol{x}}_{k \mid k}^{i}=\hat{\boldsymbol{x}}_{k \mid k-1}^{i}+\boldsymbol{P}_{k \mid k-1}^{i} \boldsymbol{H}^{\mathrm{T}}\left(\boldsymbol{H} \boldsymbol{P}_{k \mid k-1}^{i} \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{R}_{k}\right)^{-1}\left(\boldsymbol{y}_{k}-\boldsymbol{H} \hat{\boldsymbol{x}}_{k \mid k-1}^{i}\right) \\ \boldsymbol{P}_{k \mid k}^{i}=\boldsymbol{P}_{k \mid k-1}^{i}-\boldsymbol{P}_{k \mid k-1}^{i} \boldsymbol{H}^{\mathrm{T}}\left(\boldsymbol{H} \boldsymbol{P}_{k \mid k-1}^{i} \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{R}_{k}\right)^{-1} \boldsymbol{H} \boldsymbol{P}_{k \mid k-1}^{i} \end{aligned}$

条件模型概率 $p\left(r_{k}=i \mid \boldsymbol{y}^{k}\right)$ 为

$\begin{aligned} \mu_{k \mid k}(i)=\frac{p\left(\boldsymbol{y}_{k} \mid r_{k}=i, \boldsymbol{y}^{k-1}\right) p\left(r_{k}=i \mid \boldsymbol{y}^{k-1}\right)}{p\left(\boldsymbol{y}_{k} \mid \boldsymbol{y}^{k-1}\right)} \end{aligned}$

经简化可得

$\begin{aligned} \mu_{k \mid k}(i)=\frac{\lambda_{k}(i) \sum_{j=1}^{d} \Gamma_{j i} \mu_{k-1 \mid k-1}(j)}{\sum_{l=1}^{d} \lambda_{k}(l) \sum_{m=1}^{d} \Gamma_{m l} \mu_{k-1 \mid k-1}(m)} \end{aligned}$

IMM迭代计算方程

for 对于每一个模型 i do
模型预测概率 $\mu_{k \mid k-1}(i)=p\left(r_{k}=i \mid y^{k-1}\right)=\sum_{j=1}^{d} \Gamma_{ji} \mu_{k-1 \mid k-1}(j)$ 混合模型概率 $\begin{aligned} \mu_{k \mid k-1}^{j \mid i}=p\left(r_{k-1}=j \mid r_{k}=i, y^{k-1}\right)=\frac{\Gamma_{ji} \mu_{k-1 \mid k-1}(j)}{\sum_{m=1}^{d} \Gamma_{m i} \mu_{k-1 \mid k-1}(m)} \end{aligned}$ 混合状态和协方差 $\hat{\boldsymbol{x}}_{k-1 \mid k-1}^{0 i}=\sum_{j=1}^{d}\mu_{k \mid k-1}^{j \mid i}\hat{\boldsymbol{x}}_{k-1 \mid k-1}^{j}$ $\boldsymbol{P}_{k-1 \mid k-1}^{0 i}=\sum_{j=1}^{d} \boldsymbol{\mu}_{k \mid k-1}^{j \mid i}\left\{\boldsymbol{P}_{k-1 \mid k-1}^{j}+\left[\hat{\boldsymbol{x}}_{k-1 \mid k-1}^{j}-\boldsymbol{x}_{k-1 \mid k-1}^{0 i}\right]\left[\hat{\boldsymbol{x}}_{k-1 \mid k-1}^{j}-\hat{\boldsymbol{x}}_{k-1 \mid k-1}^{0 i}\right]^{\mathrm{T}}\right\}$ end for
for 对于每一个模型 i do
预测目标状态 $\hat{\boldsymbol{x}}_{k \mid k-1}^{i}=\boldsymbol{F}_{i} \hat{\boldsymbol{x}}_{k-1 \mid k-1}^{0 i}+\boldsymbol{u}_{i}$ 预测协方差 $\boldsymbol{P}_{k \mid k-1}^{i}=\boldsymbol{F}_{i} \boldsymbol{P}_{k-1 \mid k-1}^{0 i} \boldsymbol{F}_{i}^{T}+\boldsymbol{Q}_{i}$ 状态更新 $\hat{\boldsymbol{x}}_{k \mid k}^{i}=\hat{\boldsymbol{x}}_{k \mid k-1}^{i}+\boldsymbol{P}_{k \mid k-1}^{i} \boldsymbol{H}^{T}\left(\boldsymbol{H} \boldsymbol{P}_{k \mid k-1}^{i} \boldsymbol{H}^{T}+\boldsymbol{R}_{k}\right)^{-1}\left(\boldsymbol{y}_{k}-\boldsymbol{H} \hat{\boldsymbol{x}}_{k \mid k-1}^{i}\right)$ 协方差更新 $\boldsymbol{P}_{k \mid k}^{i}=\boldsymbol{P}_{k \mid k-1}^{i}-\boldsymbol{P}_{k \mid k-1}^{i} \boldsymbol{H}^{\mathrm{T}}\left(\boldsymbol{H} \boldsymbol{P}_{k \mid k-1}^{i} \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{R}_{k}\right)^{-1} \boldsymbol{H} \boldsymbol{P}_{k \mid k-1}^{i}$ 模型似然函数 $\lambda_{k}(i)=N\left(\boldsymbol{y}_{k} ; \boldsymbol{H} \hat{\boldsymbol{x}}_{k \mid k-1}^{i}, \boldsymbol{H} \boldsymbol{P}_{k \mid k-1}^{i} \boldsymbol{H}^{T}+\boldsymbol{R}_{k}\right)$ end for
模型概率： $\begin{aligned} \mu_{k \mid k}(i)=\frac{\lambda_{k}(i) \sum_{j=1}^{d} \Gamma_{j i} \mu_{k-1 \mid k-1}(j)}{\sum_{l=1}^{d} \lambda_{k}(l) \sum_{m=1}^{d} \Gamma_{m l} \mu_{k-1 \mid k-1}(m)} \end{aligned}$ 条件均值： $\hat{\boldsymbol{x}}_{k \mid k}=\sum_{i=1}^{d} \hat{\boldsymbol{x}}_{k \mid k}^{i} \boldsymbol{\mu}_{k \mid k}(i)$ 条件协方差： $\boldsymbol{P}_{k \mid k}=\sum_{i=1}^{d}\left[\boldsymbol{P}_{k \mid k}^{i}+\left(\hat{\boldsymbol{x}}_{k \mid k}-\hat{\boldsymbol{x}}_{k \mid k}^{i}\right)\left(\hat{\boldsymbol{x}}_{k \mid k}-\hat{\boldsymbol{x}}_{k \mid k}^{i}\right)^{\mathrm{T}}\right] \boldsymbol{\mu}_{k \mid k}(i)$

仿真

clc;close all;clear all;

simTime=100;      %仿真迭代次数
T=1;

d = 3;%模型数

w2=3*2*pi/360;     %模型2转弯率3度
w3=-3*2*pi/360;    %模型3转弯率-3度
H=[1,0,0,0;0,0,1,0];                      %模型量测矩阵
G=[T^2/2,0;T,0;0,T^2/2;0,T];              %模型过程噪声加权矩阵
r=100;                                 %20 2000
R=[r,0;0,r];                           %模型量测噪声协方差矩阵
Q=G*[10,0;0,10]*G';                      %模型过程噪声协方差矩阵

F(:,:,1)=[1,T,0,0;0,1,0,0;0,0,1,T;0,0,0,1];     %模型1状态转移矩阵

F(:,:,2)=[1,sin(w2*T)/w2,0,(cos(w2*T)-1)/w2;
    0,cos(w2*T),0,sin(w2*T);
    0,(1-cos(w2*T))/w2,1,sin(w2*T)/w2;
    0,-sin(w2*T),0,cos(w2*T)];            %模型2状态转移矩阵 左转弯

F(:,:,3)=[1,sin(w3*T)/w3,0,(cos(w3*T)-1)/w3;
    0,cos(w3*T),0,sin(w3*T);
    0,(1-cos(w3*T))/w3,1,sin(w3*T)/w3;
    0,-sin(w3*T),0,cos(w3*T)];            %模型3状态转移矩阵 右转弯

x = zeros(4,simTime);
z_k = zeros(2,simTime);         %含噪声量测数据
measureNoise = zeros(2,simTime);
measureNoise = sqrt(R)*randn(2,simTime);  %产生量测噪声
x(:,1)=[1000,200,1000,200]';
z_k(:,1)=H*x(:,1)+measureNoise(:,1);
for a=2:simTime
    if (a>=20)&&(a<=40) 
        x(:,a)=F(:,:,2)*x(:,a-1);      %20--40s左转 
    elseif (a>=60)&&(a<=80) 
       x(:,a)=F(:,:,3)*x(:,a-1);        %60--80s右转 
    else
        x(:,a)=F(:,:,1)*x(:,a-1);      %匀速直线运动
    end
z_k(:,a)=H*x(:,a)+measureNoise(:,a);
end

xkki(:,1) = x(:,1);      %模型1IMM算法状态估计值
xkki(:,2) = x(:,1);      %模型2IMM算法状态估计值
xkki(:,3) = x(:,1);      %模型3IMM算法状态估计值

xkk = zeros(4,simTime);      %IMM算法模型综合状态估计值
pkk=zeros(4,4,simTime);      %IMM算法模型综合状态协方差矩阵
pkki(:,:,1)=zeros(4,4);
pkki(:,:,2)=zeros(4,4);
pkki(:,:,3)=zeros(4,4);      %IMM算法各模型协方差矩阵

xkk(:,1)=x(:,1);

Sigmaji=[0.9,0.05,0.05;
         0.1,0.8,0.1;
         0.05,0.15,0.8];    %模型转移概率矩阵

ukk=zeros(3,simTime);
ukk(:,1)=[0.3 0.3 0.4]';  %IMM算法模型概率

for t=1:simTime-1
    
    %第一步Interacting（只针对IMM算法）
    ukk_1=Sigmaji'*ukk(:,t);
    
    for i = 1:d
        uji(:,i)=(1/ukk_1(i))*Sigmaji(:,i).*ukk(:,t);%计算模型混合概率     
    end

    % 计算各模型滤波初始化条件
    % 各模型滤波初始状态
    for i = 1:d
        x0(:,i) = xkki * uji(:,i);
    end 
    
    %各模型滤波初始状态协方差矩阵
    for i = 1:d
        temp = zeros(4,4);
        for k = 1:d
            temp = temp + pkki(:,:,k)+(xkki(:,i)-x0(:,i))*(xkki(:,i)-x0(:,i))'*uji(k,i);
        end
        P0(:,:,i) = temp;  
    end
    
    % kalman滤波并且计算似然函数值
    for i = 1:d
        [xkki(:,i),pkki(:,:,i),xkk_1,pkk_1] = Kalman(z_k(:,t),x0(:,i),F(:,:,i),H,P0(:,:,i),Q,R);
        lambda(i) = (1/sqrt(abs(2*pi*(det(H*pkk_1*H'+R)))))*exp((-1/2)*((z_k(:,t)-H*xkk_1)'*inv(H*pkk_1*H'+R)*(z_k(:,t)-H*xkk_1)));
    end
    lambda = lambda/sum(lambda);
%     条件模型概率
    for i = 1:d
        ukk(i,t+1) = lambda(i) * ukk_1(i)./lambda*ukk_1;
    end
    ukk(:,t+1) = ukk(:,t+1)/sum(ukk(:,t+1));
%     ukk(:,t+1) = 1/(lambda*ukk_1).*lambda'.*ukk_1;
    xkk(:,t+1) = xkki * ukk(:,t+1);
end

figure
hold on
grid on
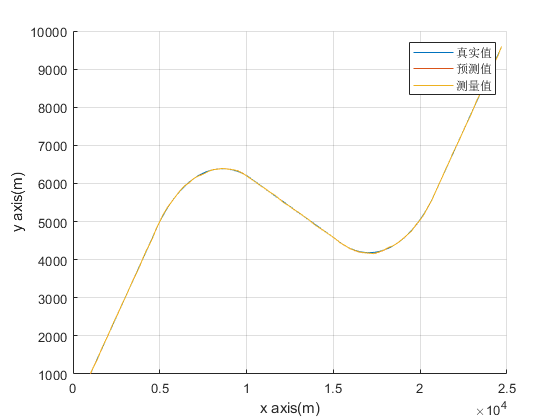
plot(x(1,:),x(3,:));
plot(xkk(1,:),xkk(3,:));
plot(z_k(1,:),z_k(2,:));
xlabel('x axis(m)');
ylabel('y axis(m)');
legend('真实值','预测值','测量值');

figure
hold on
grid on
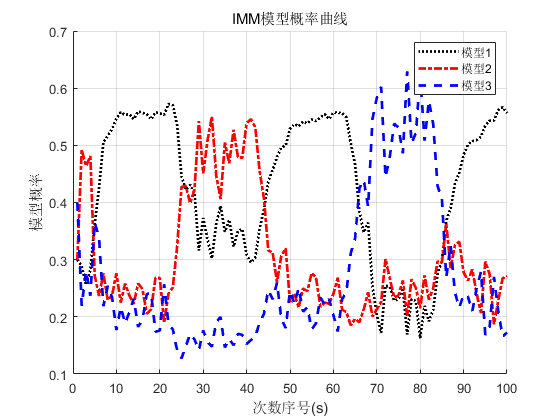
plot(ukk(1,:),'k:','linewidth',2);
plot(ukk(2,:),'r-.','linewidth',2);
plot(ukk(3,:),'b--','linewidth',2);
title('IMM模型概率曲线');
xlabel('次数序号(s)'); ylabel('模型概率');
legend('模型1','模型2','模型3');

function [x_est,P_k_k,x_pre,P] = Kalman(z_k,x_est_k_minus1,F,H,P_k,Q,R)
   x_pre = F*x_est_k_minus1;
   P = F*P_k*F' + Q;
   
   z_pre = H*x_pre;
   S = H*P*H' + R;
   K = P*H'/(S);
   
   x_est = x_pre + K*(z_k - z_pre);
   P_k_k = (eye(size(K*H,1))-K*H)*P;
end

UKF

发表于 2020-06-30 更新于 2021-05-08 分类于 Tracking

不敏卡尔曼滤波

首先讨论这样的一个问题一个满足高斯分布的随机变量经过非线性系统的输出随机变量的分布如何确定呢？
如果采用蒙特卡洛估方法。下图，在原高斯分布中采样，很多采样点（该图中是500000个画出来的），将采样点通过非线性变换，再统计变换后的结果的均值与方差，近似用一个高斯分布表示。这种方法的缺点很明显，计算量巨大，特别是在高维时。

或者说我们如何得到输出变量的一阶二阶标准矩？
考虑一个随机变量 $\boldsymbol{x} \in \mathbb{R}^{n}$ 和非线性变换 $\boldsymbol{g}: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$。$z$的均值可以表示为

$E(z)=\int g(\boldsymbol{x}) p(\boldsymbol{x}) d \boldsymbol{x}$

实际上这样的计算在大多数情况下是无法计算的（工程）。
而在目标跟踪的过程中其实只要能够数值近似$E(z)$和$D(z)$,在这里采用不敏变换

不敏变换（UT）

基本思路：通过定义域上非均匀采样点的函数值进行加权求和

UT变换的步骤：

Choose Sigma Points
Transform Sigma Points
Compute Weighted Mean And Covariance of Transformed Sigma Points

Choose Sigma Points

$N$维的高斯分布选择$2N+1$个Sigma点$\chi^{1},\chi^{2}\cdots \chi^{2N+1}$，$w^{1}，w^{2}\cdots w^{2N+1}$表示对应的权值，要求Sigma点的均值方差收敛于原均值与方差

$\begin{array}{l} \frac{1}{2N+1} \sum_{i=1}^{2N+1} w^{i} \chi^{i}=E(\boldsymbol{x}) \\ \frac{1}{2N+1} \sum_{i=1}^{2N+1} w^{i}\left[\chi^{i}-E(\boldsymbol{x})\right]\left[\chi^{i}-E(\boldsymbol{x})\right]^{\mathrm{T}}=\operatorname{cov}(\boldsymbol{x}) \end{array}$

令 ${Z}^{i}=\boldsymbol{g}\left(\chi^{i}\right), i=1, \cdots, 2N+1$ 表示在第 $i$ 个 $\operatorname{sigma}$ 点处的函数值。 $z$ 均值的 UT $\mathbb{近}$
似可以表示为

$\widehat{E(z)}=\frac{1}{2N+1} \sum_{i=1}^{2N+1} w^{i} {Z}^{i}$

z的协方差矩阵以及 z 和 x 的互协方差，通过 UT 近似计算可以得到

$\begin{aligned} \widehat{\operatorname{cov}(z)} &=\frac{1}{2N+1} \sum_{i=1}^{2N+1} w^{i}\left[Z^{i}-\widehat{E(z)}\right]\left[{Z}^{i}-\widehat{E(z)}\right]^{\mathrm{T}} \\ \widehat{\operatorname{cov}(x, z)} &=\frac{1}{2N+1} \sum_{i=1}^{2N+1} w^{i}\left[\chi^{i}-E(x)\right]\left[{Z}^{i}-\widehat{E(z)}\right]^{\mathrm{T}} \end{aligned}$

Sigma点的选择有很多种在这里选择，采用如下的方法：

$\chi^{i} = \boldsymbol{\mu} + \boldsymbol{\sigma}^{i}$

其中

$\boldsymbol{\mu}=E(\boldsymbol{x})$
$\boldsymbol{\sigma}^{1} = \boldsymbol{0}$，$[\boldsymbol{\sigma}^{2} \cdots \boldsymbol{\sigma}^{N+1}] = \boldsymbol{A}(\boldsymbol{\sigma}^{N+i+1}=-\boldsymbol{\sigma}^{i+1}, i=1, \cdots, N)$,$\boldsymbol{A}$是$(N+\kappa)\boldsymbol{\Sigma}$的Cholesky分解，即满足$\boldsymbol{A}\boldsymbol{A}^T=(N+\kappa)\boldsymbol{\Sigma}$

$\chi^{i}$对应的权值为

$w^{i}=\left\{\begin{array}{ll} \kappa /(N+\kappa) & i=1 \\ 0.5 /(N+\kappa) & i=2, \cdots, 2 N+1 \end{array}\right.$

用图像可以形象的表示出来(2维的情况)

不敏卡尔曼滤波算法

(1) 确定 sigma 点 $\chi_{k-1}^{1}, \cdots, \chi_{k-1}^{2N+1}$ 和权值 $w^{1}, \cdots, w^{2N+1}$
(2) 计算 sigma 点的转换 $\chi_{k}^{i}=f\left(\chi_{k-1}^{i}\right), i=1, \cdots, 2N+1$。
(3) 计算状态预测统计量

$\begin{array}{c} \hat{\boldsymbol{x}}_{k \mid k-1}=\sum_{i=1}^{2N+1} w^{i} \chi_{k}^{i} \\ \boldsymbol{P}_{k \mid k-1}=\boldsymbol{Q}_{k}+\sum_{i=1}^{2N+1} w^{i}\left(\chi_{k}^{i}-\hat{\boldsymbol{x}}_{k \mid k-1}\right)\left(\chi_{k}^{i}-\hat{\boldsymbol{x}}_{k \mid k-1}\right)^{\mathrm{T}} \end{array}$

(4) 确定均值 $\hat{\boldsymbol{x}}_{k \mid k-1}$ 和方差 $\boldsymbol{P}_{k \mid k-1}$ 的 $\operatorname{sigma}$ 点 $\chi_{k}^{1}, \cdots, \chi_{k}^{2N+1}$ 和权值 $w^{1}, \cdots, w^{2N+1}$
(5) 计算 sigma 点的转换 $\nu_{k}^{i}=\boldsymbol{h}\left(\chi_{k}^{i}\right), i=1, \cdots, 2N+1$。
(6)计算观测预测统计量

$\begin{array}{l} \hat{\boldsymbol{y}}_{k \mid k-1}=\sum_{i=1}^{2N+1} w^{i} \boldsymbol{\nu}_{k}^{i} \\ \boldsymbol{S}_{k}=\boldsymbol{R}_{k}+\sum_{i=1}^{2N+1} w^{i}\left(\nu_{k}^{i}-\hat{\boldsymbol{y}}_{k \mid k-1}\right)\left(\nu_{k}^{i}-\hat{\boldsymbol{y}}_{k \mid k-1}\right)^{\mathrm{T}} \\ \boldsymbol{\Psi}_{k}=\sum_{i=1}^{2N+1} w^{i}\left(\chi_{k}^{i}-\hat{\boldsymbol{x}}_{k \mid k-1}\right)\left(\nu_{k}^{i}-\hat{\boldsymbol{y}}_{k \mid k-1}\right)^{\mathrm{T}} \end{array}$

(7) 计算后验均值和方差矩阵

$\begin{aligned} \hat{\boldsymbol{x}}_{k} &=\hat{\boldsymbol{x}}_{k \mid k-1}+\boldsymbol{\Psi}_{k} \boldsymbol{S}_{k}^{-1}\left(\boldsymbol{y}_{k}-\hat{\boldsymbol{y}}_{k \mid k-1}\right) \\ \boldsymbol{P}_{k \mid k}&= \boldsymbol{P}_{k \mid k-1}-\boldsymbol{\Psi}_{k} \boldsymbol{S}_{k}^{-1} \boldsymbol{\Psi}_{k}^{\mathrm{T}} \end{aligned}$

KF

发表于 2020-06-29 更新于 2021-05-08 分类于 Tracking

卡尔曼滤波

假设条件

A1 目标动态和观测方程是线性的：

$\begin{array}{l} \mathbf{x}_{k}= \mathbf{F} \mathbf{x}_{k-1}+\mathbf{v}_{k} \\ \mathbf{y}_{k}=\mathbf{H} x_{k}+\mathbf{w}_{k} \end{array}$

A2 $\mathbf{v}_{k}$ 和 $\mathbf{w}_{k}$ 是均值为突且噪声协方差分别为 $\mathbf{Q}_{k}$ 和 $\mathbf{R}_{k}$ 的高斯白噪声
A3 $k-1$ 时刻后验概率密度 $p\left(\mathbf{x}_{k-1} \mid \mathbf{y}^{k-1}\right)$ 是均值为 $\hat{\mathbf{x}}_{k-1| k-1}$，方差为$\mathbf{P}_{k-1 | k-1}$的高斯形式。

高斯分布与高斯乘积定理

首先规定一下高斯密度函数，由于求解后验概率密度时需要有概率密度函数相乘，所以我们很感兴趣两个概率密度函数相乘后满足怎样的分布

$N(z ; \mathbf{\mu}, \mathbf{\Sigma})=\frac{1}{\sqrt{2 \pi|\mathbf{\Sigma}| }} \exp \left[-(z-\mathbf{\mu})^{\mathrm{T}} \mathbf{\Sigma}^{-1}(z-\mathbf{\mu}) / 2\right]$

高斯乘积定理: 给定 $\mathbf{x}_{1}, \mathbf{\mu}_{1} \in \mathbb{R}^{d_{1}}, \mathbf{H} \in \mathbb{R}^{d_{2} \times d_{1}}, \mathbf{x}_{2} \in \mathbb{R}^{d_{2}}$ 和正定矩阵$\mathbf{P}_{1}, \mathbf{P}_{2}$

$N\left(\mathbf{x}_{2} ; \mathbf{H} \mathbf{x}_{1}, \mathbf{P}_{2}\right) N\left(\mathbf{x}_{1} ; \mathbf{\mu}_{1}, \mathbf{P}_{1}\right)=N\left(\mathbf{x}_{2} ; \mathbf{H} \mathbf{\mu}_{1}, \mathbf{P}_{3}\right) N\left(\mathbf{x}_{1} ; \mathbf{\mu}, \mathbf{P}\right)$

其中

$\begin{array}{c} \mathbf{P}_{3}=\mathbf{H} \mathbf{P}_{1} \mathbf{H}^{\mathrm{T}}+\mathbf{P}_{2} \\ \mathbf{\mu}=\mathbf{\mu}_{1}+\mathbf{K}\left(\mathbf{x}_{2}-\mathbf{H} \mathbf{\mu}_{1}\right) \\ \mathbf{P}=\mathbf{P}_{1}+\mathbf{K} \mathbf{H} \mathbf{P}_{1} \\ \mathbf{K}=\mathbf{P}_{1} \mathbf{H}^{\mathrm{T}} \mathbf{P}_{3}^{-1} \end{array}$

卡尔曼迭代

预测函数

状态转移函数

$p\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{k-1}\right)=N\left(\boldsymbol{x}_{k} ; \boldsymbol{F} \boldsymbol{x}_{k-1}, \boldsymbol{Q}_{k}\right)$

假定$k-1$时刻的目标状态后验概率密度函数$p(\boldsymbol{x}_{k-1} | \boldsymbol{y}^{k-1}) = N(\boldsymbol{x}_{k-1};\left.\hat{\boldsymbol{x}}_{k-1 \mid k-1}, \boldsymbol{P}_{k-1 \mid k-1}\right)$

预测概率密度函数

$\begin{aligned} p\left(\boldsymbol{x}_{k} \mid \boldsymbol{y}^{k-1}\right) &=\int p\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{k-1}\right) p\left(\boldsymbol{x}_{k-1} \mid \boldsymbol{y}^{k-1}\right) \mathrm{d} \boldsymbol{x}_{k-1} \\ &=\int N\left(\boldsymbol{x}_{k} ; \boldsymbol{F} \boldsymbol{x}_{k-1}, \boldsymbol{Q}_{k}\right) N\left(\boldsymbol{x}_{k} ; \hat{\boldsymbol{x}}_{k-1 \mid k-1}, \boldsymbol{P}_{k \mid k-1}\right) \mathrm{d} \boldsymbol{x}_{k-1} \end{aligned}$

应用高斯乘积定理，可以得到预测概率密度的表达式为

$\begin{aligned} p\left(\boldsymbol{x}_{k} \mid \boldsymbol{y}^{k-1}\right)=& \int N\left(\boldsymbol{x}_{k} ; \hat{\boldsymbol{x}}_{k \mid k-1}, \boldsymbol{P}_{k \mid k-1}\right) \times \\ & N\left(\boldsymbol{x}_{k-1} ; \hat{\boldsymbol{x}}_{k-1 \mid k-1}+G_{k}\left(\boldsymbol{x}_{k}-\hat{\boldsymbol{x}}_{k \mid k-1}\right), \boldsymbol{M}_{k}\right) \mathrm{d} \boldsymbol{x}_{k-1} \\ =& N\left(\boldsymbol{x}_{k} ; \hat{\boldsymbol{x}}_{k \mid k-1}, \boldsymbol{P}_{k \mid k-1}\right) \end{aligned}$

这一操作即为标准卡尔曼滤波预测，其伪函数形式可写为

$\left[\hat{\boldsymbol{x}}_{k \mid k-1}, \boldsymbol{P}_{k \mid k-1}\right]=K F_{p}\left[\hat{\boldsymbol{x}}_{k-1 \mid k-1}, \boldsymbol{P}_{k-1 \mid k-1}, \boldsymbol{F}, \boldsymbol{Q}\right]$

其中

$\begin{array}{c} \hat{\boldsymbol{x}}_{k \mid k-1}=\boldsymbol{F} \hat{\boldsymbol{x}}_{k-1 \mid k-1} \\ \boldsymbol{P}_{k \mid k-1}=\boldsymbol{F} \boldsymbol{P}_{k-1 \mid k-1} \boldsymbol{F}^{\mathrm{T}}+\boldsymbol{Q} \end{array}$

似然函数与归一化因子

似然函数：$p( \boldsymbol{y}_{k}\mid \boldsymbol{x}_{k}) = N(\boldsymbol{y}_{k};\boldsymbol{Hx}_k,\boldsymbol{R}_k)$

归一化因子：

$\begin{array}{c} p\left(\boldsymbol{y}^{k} \mid \boldsymbol{y}^{k-1}\right) =\int p\left(\boldsymbol{y}_{k} \mid \boldsymbol{x}_{k}\right) p\left(\boldsymbol{x}_{k} \mid \boldsymbol{y}^{k-1}\right) \mathrm{d} \boldsymbol{x}_{k} \\ =\int N\left(\boldsymbol{y}_{k} ; \boldsymbol{H} \boldsymbol{x}_{k}, \boldsymbol{R}_{k}\right) N\left(\boldsymbol{x}_{k} ; \hat{\boldsymbol{x}}_{k / k-1}, \boldsymbol{P}_{k \mid k-1}\right) \mathrm{d} \boldsymbol{x}_{k} \\ =N\left(\boldsymbol{y}_{k} ; \boldsymbol{y}_{k \mid k-1}, \boldsymbol{S}_{k}\right) \end{array}$

其中$\hat{\boldsymbol{y}}_{k \mid k-1}=\boldsymbol{H} \hat{\boldsymbol{x}}_{k \mid k-1}, \boldsymbol{S}_{k}=\boldsymbol{H} \boldsymbol{P}_{k \mid k-1} \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{R}_{k}$

后验概率密度函数

$p\left(\boldsymbol{x}_{k} \mid \boldsymbol{y}^{k}\right)=\frac{N\left(\boldsymbol{y}_{k} ; \boldsymbol{H} \boldsymbol{x}_{k}, \boldsymbol{R}_{k}\right) N\left(\boldsymbol{x}_{k} ; \hat{\boldsymbol{x}}_{k \mid k-1}, \boldsymbol{P}_{k \mid k-1}\right)}{N\left(\boldsymbol{y}_{k} ; \boldsymbol{y}_{k \mid k-1}, \boldsymbol{S}_{k}\right)}$

再次利用高斯乘积定理，后验概率密度可以表示为

$\begin{array}{c} p\left(\boldsymbol{x}_{k} \mid \boldsymbol{y}^{k}\right)=N\left(\boldsymbol{x}_{k} ; \hat{\boldsymbol{x}}_{k \mid k}, \boldsymbol{P}_{k \mid k}\right) \end{array}$

其中

$\hat{\boldsymbol{x}}_{k \mid k}=\hat{\boldsymbol{x}}_{k \mid k-1}+\boldsymbol{P}_{k \mid k-1} \boldsymbol{H}^{\mathrm{T}} \boldsymbol{S}_{k}^{-1}\left(\boldsymbol{y}_{k}-\hat{\boldsymbol{y}}_{k \mid k-1}\right) \\ \boldsymbol{P}_{k \mid k}=\boldsymbol{P}_{k \mid k-1}-\boldsymbol{P}_{k \mid k-1} \boldsymbol{H}^{\mathrm{T}} \boldsymbol{S}_{k}^{-1} \boldsymbol{H} \boldsymbol{P}_{k \mid k-1}$

到这里其实卡尔曼滤波的迭代估计就结束了，接下来给出一个算法的流程

算法流程

卡尔曼滤波方程：

计算预测均值和方差矩阵
$\begin{array}{c} \hat{\boldsymbol{x}}_{k \mid k-1}=\boldsymbol{F} \hat{\boldsymbol{x}}_{k-1 \mid k-1} \\ \boldsymbol{P}_{k \mid k-1}=\boldsymbol{F} \boldsymbol{P}_{k-1 \mid k-1} \boldsymbol{F}^{\mathrm{T}}+\boldsymbol{Q}_{k} \end{array}$
计算观测预测、新息方差矩阵和卡尔曼滤波增益
$\begin{array}{c} \hat{\boldsymbol{y}}_{k \mid k-1}=\boldsymbol{H} \hat{\boldsymbol{x}}_{k \mid k-1}\\ \boldsymbol{S}_{k}=\boldsymbol{H} \boldsymbol{P}_{k \mid k-1} \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{R} \\ \boldsymbol{K}_{k}=\boldsymbol{P}_{k \mid k-1} \boldsymbol{H}^{\mathrm{T}} \boldsymbol{S}_{k}^{-1} \end{array}$
计算后验均值和方差矩阵
$\begin{array}{c} \hat{\boldsymbol{x}}_{k \mid k}=\hat{\boldsymbol{x}}_{k \mid k-1}+\boldsymbol{K}_{k}\left(\boldsymbol{y}_{k}-\hat{\boldsymbol{y}}_{k \mid k-1}\right)\\ \boldsymbol{P}_{k \mid k}=\left(\boldsymbol{I}-\boldsymbol{K}_{k} \boldsymbol{H}\right) \boldsymbol{P}_{k \mid k-1} \end{array}$

matlab仿真

根据算法流程可以写出KalmanFilter的一步迭代函数

function [x_est,P_k_k] = KalmanFilter(z_k,x_est_k_minus1,F,H,P_k,Q,R)
   x_pre = F*x_est_k_minus1;
   P = F*P_k*F' + Q;
   
   z_pre = H*x_pre;
   S = H*P*H' + R;
   K = P*H'/(S);
   
   x_est = x_pre + K*(z_k - z_pre);
   P_k_k = (eye(size(K*H,1))-K*H)*P;
end

参数的解释
输入参数:

$z_k$ $k$时刻的量测值
$x_est_k_minus1$ $k-1$时刻的状态后验估计
$F$ 系统状态转移矩阵
$H$ 量测矩阵
$P_k$ $k-1$时刻的状态后验估计协方差矩阵
$Q$ 过程噪声协方差矩阵
$R$ 测量噪声协方差矩阵
输出参数:
$x_est$ $k$时刻状态后验估计
$P_k_k$ $k$时刻状态后验估计协方差矩阵

下面给出一个实际代码的示例

clc;close all;clear all

for kk = 1:100

T = 0.01;
L = 1000;

F = [1 T;
     0 1];
x(:,1) = [0;1];
y(1) = randn;

H = [1 0];

v = randn(1,L);
w = 1*randn(1,L);

for i =2:L
    x(:,i) = F*x(:,i-1)+[T^2/2;T]*v(i);
    y(i) = H*x(:,i)+w(i); 
end

Q =[1/3*T^3 1/2*T^2; 1/2*T^2 T]*var(v);
R = 2*var(w);

xe = zeros(2,L);
xe(:,1) = randn(2,1);
P = eye(2);

xe = zeros(2,L);

for i=2:L
    [xe(:,i),P] = KalmanFilter(y(i),xe(:,i-1),F,H,P,Q,R);
end

Err_e(kk,:) = xe(1,:)-x(1,:);
Err_m(kk,:) = w;

end

%% 对最后一次结果进行展示
figure
hold on
plot(y(1,:),'g');
plot(xe(1,:),'linewidth',2);
plot(x(1,:));
legend('测量位置','预测位置','实际位置');
xlabel('时间序号（0.01s）');
ylabel('距离（m）');
title('kalman滤波位置估计')

figure
hold on
plot(xe(2,:));
plot(x(2,:));
legend('预测速度','实际速度');
xlabel('时间序号（0.01s）');
ylabel('速度（m/s）');
title('kalman滤波速度估计')
%% 计算状态估计误差

Var_E = var(mean(Err_e));
Var_M = var(mean(Err_m));

figure
hold on
plot(abs(mean(Err_e)),'linewidth',2);
plot(abs(mean(Err_m)));
legend('测量误差','预测误差');
xlabel('时间序号（0.01s）');
ylabel('误差（m）');
title(['误差分析 Var_{exp}=' num2str(Var_E) ' Var_{M}=' num2str(Var_M) ' Monte Carlo method(100)'] );

运行可以得到

最优贝叶斯滤波

发表于 2020-06-28 更新于 2021-04-01 分类于 Tracking

贝叶斯推理

贝叶斯定理

$p(\mathbf{x}|\mathbf{y} ) = \frac{p(\mathbf{x},\mathbf{y})}{p(\mathbf{y})}$

再次利用该式可以重写为

$p(\mathbf{x}|\mathbf{y} ) = \frac{p(\mathbf{y}|\mathbf{x})p(\mathbf{x})}{p(\mathbf{y})}$

通常称$p(\mathbf{x})$为先验分布，$p(\mathbf{y}|\mathbf{x})$为最大似然估计分布，$p(\mathbf{x}|\mathbf{y})$为后验分布。

目标跟踪中的贝叶斯递推

$\mathbf{S}_k$为$k$时刻的广义目标状态。
联合概率密度函数$p(\mathbf{S}^k) =p(\mathbf{S}_0,\cdots, \mathbf{S}_k)$。
传感器输出$\mathbf{y}^{k}=(\mathbf{y}_{1}, \mathbf{y}_{2}, \cdots, \mathbf{y}_{k})$。

由贝叶斯定理

$p\left(\mathbf{S}^{k} \mid \mathbf{y}^{k}\right)=\frac{p\left(\mathbf{y}^{k} \mid \mathbf{S}^{k}\right) p\left(\mathbf{S}^{k}\right)}{p\left(\mathbf{y}^{k}\right)}$

归一化因子计算：

$p\left(\mathbf{y}^{k}\right)=\int_{\mathbf{S}_{k}} \cdots \int_{\mathbf{S}_{0}} p\left(\mathbf{y}^{k} \mid \mathbf{S}_{k}, \cdots, \mathbf{S}_{o}\right) p\left(\mathbf{S}_{k}, \cdots, \mathbf{S}_{o}\right) \mathrm{d} \mathbf{S}_{k} \cdots \mathrm{d} \mathbf{S}_{o}$

贝叶斯递推：

$\begin{aligned} & p\left(\mathbf{y}^{k} \mid \mathbf{S}^{k}\right)=p\left(\mathbf{y}_{k}, \mathbf{y}^{k-1} \mid \mathbf{S}^{k}\right) \\ & =p\left(\mathbf{y}_{k} \mid \mathbf{y}^{k-1}, \mathbf{S}^{k}\right) p\left(\mathbf{y}^{k-1} \mid \mathbf{S}^{k}\right) =p\left(\mathbf{y}_{k} \mid \mathbf{y}^{k-1}, \mathbf{S}^{k}\right) p\left(\mathbf{y}^{k-1} \mid \mathbf{S}^{k-1}\right)\\ & p\left(\mathbf{S}^{k}\right) =p\left(\mathbf{S}_{k}, \mathbf{S}^{k-1}\right)=p\left(\mathbf{S}_{k} \mid \mathbf{S}^{k-1}\right) p\left(\mathbf{S}^{k-1}\right) \\ & p\left(\mathbf{y}^{k}\right) =p\left(\mathbf{y}_{k}, \mathbf{y}^{k-1}\right)=p\left(\mathbf{y}_{k} \mid \mathbf{y}^{k-1}\right) p\left(\mathbf{y}^{k-1}\right) \end{aligned}$

带入

$p\left(\mathbf{S}^{k} \mid \mathbf{y}^{k}\right)=\frac{p\left(\mathbf{y}_{k} \mid \mathbf{y}^{k-1}, \mathbf{S}^{k}\right) p\left(\mathbf{S}_{k} \mid \mathbf{S}^{k-1}\right)}{p\left(\mathbf{y}_{k} \mid \mathbf{y}^{k-1}\right)}\left\{\frac{p\left(\mathbf{y}^{k-1} \mid \mathbf{S}^{k-1}\right) p\left(\mathbf{S}^{k-1}\right)}{p\left(\mathbf{y}^{k-1}\right)}\right\}$ $p\left(\mathbf{S}^{k} \mid \mathbf{y}^{k}\right)=\frac{p\left(\mathbf{y}_{k} \mid \mathbf{y}^{k-1}, \mathbf{S}^{k}\right) p\left(\mathbf{S}_{k} \mid \mathbf{S}^{k-1}\right)}{p\left(\mathbf{y}_{k} \mathbf{y}^{k-1}\right)} p\left(\mathbf{S}^{k-1} \mid \mathbf{y}^{k-1}\right)$ $p\left(\mathbf{S}^{k} \mid \mathbf{y}^{k}\right)=\frac{p\left(\mathbf{y}_{k} \mid \mathbf{S}_{k}\right)}{p\left(\mathbf{y}_{k} \mid \mathbf{y}^{k-1}\right)} p\left(\mathbf{S}_{k} \mid \mathbf{S}_{k-1}\right) p\left(\mathbf{S}^{k-1} \mid \mathbf{y}^{k-1}\right)$

通过推导可以得到

即就是

$p\left(\mathbf{S}_{k} \mid \mathbf{y}^{k}\right)=\frac{1}{p\left(\mathbf{y}_{k} \mid \mathbf{y}^{k-1}\right)} p\left(\mathbf{y}_{k} \mid \mathbf{S}_{k}\right) \int_{\mathbf{s}_{k-1}} p\left(\mathbf{S}_{k} \mid \mathbf{S}_{k-1}\right) p\left(\mathbf{S}_{k-1} \mid \mathbf{y}^{k-1}\right) \mathrm{d} \mathbf{S}_{k-1}$

非机动目标跟踪与最优滤波

发表于 2020-06-28 更新于 2021-04-01 分类于 Tracking

非机动目标跟踪与最优滤波

目标跟踪中的最优贝叶斯滤波

目标动态方程：$\mathbf{x}_k = g(\mathbf{x}_{k-1},\mathbf{v}_k)$

传感器观测方程：$\mathbf{y}_k = l(\mathbf{x}_{k},\mathbf{w}_k)$

由目标动态方程可以得到转移密度函数$p(\mathbf{x}_k \mid \mathbf{x}_{k-1})$
由传感器观测方程可以得到似然函数$p(\mathbf{y}_k \mid \mathbf{x}_k)$
要注意一点是当$g,l$都是线性并且$\mathbf{v}_k$和$\mathbf{w}_k$是高斯噪声时，$\mathbf{x}_k$的后验概率密度时高斯形式的。

一步预测

$p\left(\mathbf{x}_{k} \mid \mathbf{y}^{k-1}\right)=\int p\left(\mathbf{x}_{k} \mid \mathbf{x}_{k-1}\right) p\left(\mathbf{x}_{k-1} \mid \mathbf{y}^{k-1}\right) \mathrm{d} \mathbf{x}_{k-1}$

后验概率密度函数更新

$p\left(\mathbf{x}_{k} \mid \mathbf{y}^{k}\right)=\frac{1}{p\left(\mathbf{y}_{k} \mid \mathbf{y}^{k-1}\right)} p\left(\mathbf{y}_{k} \mid \mathbf{x}_{k}\right) p\left(\mathbf{x}_{k} \mid \mathbf{y}^{k-1}\right)$

最优非机动目标跟踪滤波

目标动态方程：$\mathbf{x}_k = f(\mathbf{x}_{k-1})+\mathbf{v}_k$
转移密度函数：$p(\mathbf{x}_{k}\mid \mathbf{x}_{k-1}) = p_{\mathbf{v}_{k}}(\mathbf{x}_k -f(\mathbf{x}_{k-1}) )$

传感器观测方程：$\mathbf{y}_k = h(\mathbf{x}_{k})+\mathbf{w}_k$
似然函数：$p(\mathbf{y}_{k}\mid \mathbf{x}_{k}) = p_{\mathbf{w}_{k}}(\mathbf{y}_k -h(\mathbf{x}_{k}) )$

计算后验概率密度函数

$p\left(x_{k} \mid y^{k}\right) =\frac{p_{w_{k}}\left(y_{k}-h\left(x_{k}\right)\right) \int p_{v_{k}}\left(x_{k}-f\left(x_{k-1}\right)\right) p\left(x_{k-1} \mid y^{k-1}\right) d x_{k-1}}{\int p_{w_{k}}\left(y_{k}-h\left(x_{k}\right)\right) p\left(x_{k} \mid y^{k-1}\right) d x_{k}}$

其中

$p\left(x_{k} \mid y^{k-1}\right) =\int p_{v_{k}}\left(x_{k}-f\left(x_{k-1}\right)\right) p\left(x_{k-1} \mid y^{k-1}\right) d x_{k-1}$

应用上式的不同假设条件有：
A1 目标动态和观测方程是线性的：

$\begin{array}{l} \mathbf{x}_{k}= \mathbf{F} \mathbf{x}_{k-1}+\mathbf{v}_{k} \\ \mathbf{y}_{k}=\mathbf{H} x_{k}+\mathbf{w}_{k} \end{array}$

PDradar

发表于 2020-03-01 更新于 2021-05-08 分类于 Radar Signal Processing

雷达信号处理基基础

脉冲体制

回波信号分析

以线性调频（LFM）为例，在一次发射周期中，发射信号相位为

$P_T = 2 \pi (f_R t + \frac{k}{2}t^2)+\phi_T$

发射时刻与接收到回波的时刻间时延为（v为径向速度且为匀速）

$\tau(t) =\frac{2(R - vt)}{c}$

接收信号相位为

$\begin{array}{c} P_R & = 2 \pi (f_R (t-\tau(t)) + \frac{k}{2} (t-\tau(t))^2)+\phi_T+\phi_R \\ & = 2 \pi (f_R (t - \frac{2R }{c}) + \frac{2v f_R t}{c} + \frac{k}{2} ((1+\frac{2v}{c})t-\frac{2R}{c})^2)+\phi_T+\phi_R \end{array}$

那么经过前级的处理可以得到中频信号的相位为

$P_{IF} = 2 \pi ((f_I-\frac{B}{2}) (t - \frac{2R }{c}) + \frac{2v f_R t}{c} + \frac{k}{2} ((1+\frac{2v}{c})t-\frac{2R}{c})^2)+\phi_{IF}$

假设再一次相参处理过程中脉冲积累数为M，那么第n次脉冲周期中（T）$1 \leq n \leq M$

$\tau_n(t) = \frac{2(R_n-vt)}{c} = \frac{2(R_0-vt- v(n-1)T)}{c}$ $\begin{array}{c} P_{IF_n} & = 2 \pi ((f_I-\frac{B}{2}) t - \frac{2R_n (f_I-\frac{B}{2})}{c} + \frac{2v f_R t}{c} + \frac{k}{2} ((1+\frac{2v}{c})t-\frac{2R_n}{c})^2)+\phi_{IF} \\ & = 2 \pi \{(f_I-\frac{B}{2}) (t - \tau_n ) + \frac{2v f_R t}{c} + \frac{k}{2} [(1+\frac{2v}{c})t-\tau_n]^2\}+\phi_{IF} \\ &(\tau_n \leq t \leq T*DR+\tau_n) \end{array}$

其中 $R_n = R_{0} - v(n-1)T$ , $\tau_n = \frac{2R_n}{c} = \tau_n(0)$,$DR$ 为占空比。

注：

$P_{IF}=P_R-P_L$,其中本振信号相位$P_D=2\pi(t-\frac{2R}c+\phi_D)(f_R-f_I+\frac B 2)$，$\phi_D$最终归入$\phi_{IF}$这个系数中，后级处理暂不考虑。
$R_n$指第n个脉冲发射时刻，目标与雷达之间的距离，因此$R_n=R_0-v(n-1)$
$\tau_n$由如下得到：
$\tau_n=\frac {2(R_n-v\frac {\tau_n} 2)}{c} \Rightarrow\tau_n=\frac{2R_n}{c+v}$
解得 $\tau_n=\frac{2R_n}{c+v}$
因此，$\tau_n=\frac{2R_n}{c+v}\approx\frac{2R_n}{c}=\frac{2(R_0-v(n-1)T)}{c}$,当$R_0 \gg v(n-1)T $时，$\tau_n \approx \tau_0$。

匹配滤波原理简述

匹配滤波器（match filter）是最佳线性滤波器的一种，该滤波器的准则是输出信噪比最大，常用于通信、雷达等系统的接收机中，下面对其冲激响应/系统函数进行推导。

设该滤波器传递函数为$H(f)$，冲激响应为$h(t)$，输入信号为

$r(t)=s(t)+n(t)$

其中$s(t)$为输入信号，$n(t)$为高斯白噪声。

设输入信号的频谱密度函数为$S(f)$，而高斯白噪声的单边功率谱为$\frac{n_0}2$，其中$n_0$为高斯白噪声单边功率谱密度。

那么经过系统响应函数为$H(j\omega)$的LTI系统后，设$s_0(t)$为信号的输出，其大小为

$s_{0}(t) = \int_{-\infty }^{+\infty}H(f)S(f)e^{j2\pi ft}df$

而又已知输出高斯白噪声的功率谱密度等于输入白噪声的功率谱密度乘以系统传递函数模值的平方，即输出噪声功率为：

$N_0 = \frac{n_0}{2}\int_{-\infty }^{+\infty }|H(f)|^{2}df$

因此，在采样时刻$t_0$上，输出信号瞬时功率和噪声平均功率之比为：

$r_0 = \frac{|s_0(t_0)|^2}{N_0}=\frac{|\int_{-\infty }^{+\infty}H(f)S(f)e^{j2\pi ft}df)|^2}{\frac{n_0}{2}\int_{-\infty }^{+\infty}|H(f)|^2df}$

利用柯西-施瓦兹不等式

$|\int_{-\infty }^{+\infty}f_1(x)f_2(x)dx|^2 \leq \int_{-\infty }^{+\infty}|f_1(x)|^2dx\int_{-\infty }^{+\infty}|f_2(x)|^2dx$

该等式当且仅当$f_1(x) = kf^{*}_{2}(x)$时取最大值,其中$k$为任意常数。那么令$f_1(x) = H(f),f_2(x)=H(f)e^{j2\pi ft_0}$可以得到：

$r_0 \leq \frac{\int_{-\infty }^{+\infty}|H(f)|^2dx\int_{-\infty }^{+\infty}|S(f)|^2dx}{\frac{n_0}{2}\int_{-\infty }^{+\infty}|H(f)|^2df} = \frac{\int_{-\infty }^{+\infty}|S(f)|^2df}{\frac{n_0}{2}} = \frac{2E}{n_0}$

其中E为信号的能量。而且当且仅当$H(f) = k S^*(f)e^{-j2\pi ft_0}$时，$r_0$取得最大值。

对$H(f)$求逆FFT变换，可得滤波器的冲激响应

$h(t) = ks^*(t_0 -t)$

由上式可知匹配滤波器的冲激响应就是信$s(t)$的镜像，只不过存在一个$t_0$的时延。
也可以将匹配滤波的过程理解为一个求相关的过程，当$t_0$时刻信号进入滤波器时，与滤波器系数进行卷积，相当于求自相关，很明显要远大于白噪声和滤波器系数的互相关，此时信噪比可达到最大。

仿真

参数设计

首先进行参数设计

c = 3e8;         %光速
RF = 35e9;       %射频频率
lambda = c/RF;   %射频波长
f0 = 85e6;       %中频  85MHz
fs = 80e6;       %采样率  80MHz
T = 50e-6;       %脉冲重复周期  500u

DutyRatio = 0.1;           %占空比
Tp = DutyRatio * T;        %脉冲持续时间  5us
tp = 0:1/fs:Tp-1/fs;
NTp = length(tp);          %脉冲采样点数

B = 10e6;         %调频带宽  10MHz
k = B/Tp;         %调频斜率=带宽/脉冲持续时间

M = 32;           %发射脉冲数/脉冲积累数

t = 0:1/fs:T-1/fs;  
NT = length(t);     %一个脉冲中的采样点数，距离门数

R1 = 5000;        %目标1距离
V1 = -10;         %目标1速度
R2 = 1000;        %目标2距离
V2 =0;            %目标2速度

回波生成

如前所述

$\begin{array}{c} P_{IF_n} = 2 \pi \{(f_I-\frac{B}{2}) (t - \tau_n ) + \frac{2v f_R t}{c} + \frac{k}{2} [(1+\frac{2v}{c})t-\tau_n]^2\}+\phi_{IF} \\ (\tau_n \leq t \leq T*DR+\tau_n) \end{array}$

生成中频信号,同时添加噪声

fd1 = 2*V1/lambda; %多普勒频率1
fd2 = 2*V2/lambda; %多普勒频率1

echo1 = zeros(M,NT); %回波
tao1 = zeros(1,M); 
N_tao1 = zeros(1,M); %取整
echo2 = zeros(M,NT); %回波
tao2 = zeros(1,M);  %多普勒
N_tao2 = zeros(1,M); %取整

echo = zeros(M,NT);

t_fd = 0:(1/fs):(T*M-1/fs);

echo1_fd = exp(1i*2*pi*fd1*t_fd); %目标1在M个脉冲内引起的连续多普勒
echo2_fd = exp(1i*2*pi*fd2*t_fd); %目标2在M个脉冲内引起的连续多普勒

AD_data = zeros(M,NT);

%% 模拟生成目标回波
for m=1:1:M
    
    tao1(1,m)=2*(R1-V1*(m-1)*T)/c;
    N_tao1(1,m) = round(tao1(1,m)*fs);
    tao2(1,m)=2*(R2-V2*(m-1)*T)/c;
    N_tao2(1,m) = round(tao2(1,m)*fs);
    
    for n=1:1:NT
        if(n < N_tao1(1,m))
            echo1(m,n) = 0;
        elseif(( n>=N_tao1(1,m) ) && ( n<=(N_tao1(1,m)+NTp) ))
            echo1(m,n) = exp(1i*pi*k*((1+2*V1/c)*t(n)-tao1(1,m)).^2)*exp(-1i*2*pi*(f0-B/2)*tao1(1,m))*exp(1i*2*pi*(f0-B/2)*t(n))*echo1_fd(1,n+(m-1)*NT);
        else
            echo1(m,n) = 0;
        end
        
         if(n < N_tao2(1,m))
            echo2(m,n) = 0;
        elseif(( n>=N_tao2(1,m) ) && ( n<=(N_tao2(1,m)+NTp) ))
            echo2(m,n) = exp(1i*pi*k*((1+2*V2/c)*t(n)-tao2(1,m)).^2)*exp(-1i*2*pi*(f0-B/2)*tao2(1,m))*exp(1i*2*pi*(f0-B/2)*t(n))*echo2_fd(1,n+(m-1)*NT);
        else
            echo2(m,n) = 0;
        end
    end
    
    %------在echo中添加高斯噪声------%
    SNR1 = -5;  % 信号1的信噪比dB
    NOISE1=randn(1,NT);
    
    signal_power1 = (1/NTp)*(sum((echo1(m,:).*conj(echo1(m,:)))));
    noise_variance1 = signal_power1 / ( 10^(SNR1/10) );
    std_noise_n1 = std(NOISE1);
    NOISE1 =1/ sqrt(noise_variance1)*NOISE1;
    echo1(m,:)=echo1(m,:)+(NOISE1+1i*hilbert(NOISE1));
    
    SNR2 = 2;  % 信号2的信噪比dB
    NOISE2=randn(1,NT);

    signal_power2 = (1/NTp)*(sum((echo2(m,:).*conj(echo2(m,:)))));
    noise_variance2 = signal_power2 / ( 10^(SNR2/10) );
    std_noise_n2 = std(NOISE2);
    NOISE2 = 1/sqrt(noise_variance1)*NOISE2;
    echo2(m,:)=echo2(m,:)+(NOISE2+1i*hilbert(NOISE2));
    %------在echo中添加高斯噪声end------%
    
    echo(m,:) = echo1(m,:)+ echo2(m,:);
    AD_data(m,:) = real( echo(m,:) );
end

数字正交下变频（DDC）

正交解调框图如下

同时对下变频信号进行匹配滤波

%% DDC

local_I = -sin(2*pi*5e6*t);   %本振
local_Q = cos(2*pi*5e6*t);    
lowpassFilter=fir1(128,1/8); 

PC_Coff = exp(-1i*pi*k*((-Tp/2:1/10e6:Tp/2).^2));
% N_FFT = 500;   %根据运行结果调整
% H2 = conj(fft(h2,N_FFT));   %匹配滤波

for m=1:1:M  
    I_data_local(m,:) = AD_data(m,:).*local_I;
    Q_data_local(m,:) = AD_data(m,:).*local_Q;
    I_data_local_FIR(m,:)=filter(lowpassFilter,1,I_data_local(m,:));
    Q_data_local_FIR(m,:)=filter(lowpassFilter,1,Q_data_local(m,:));
    
    %-----8倍抽取------%
    Dec_I(m,:)=I_data_local_FIR(m,1:8:end);
    Dec_Q(m,:)=Q_data_local_FIR(m,1:8:end);
    
    DDC_data_out(m,:) = Dec_Q(m,:) + 1i*Dec_I(m,:);
    
    %-----匹配滤波-----%
%     temp(m,:) = fft(DDC_data_out(m,:),N_FFT);
%     PC_data_fft(m,:) = temp(m,:).*H2;  
%     PC_data_ifft(m,:) = ifft(PC_data_fft(m,:),N_FFT);
    
    PC(m,:) =conv(PC_Coff,DDC_data_out(m,:));
    PC_data(m,:) = PC(m,(length(PC_Coff)+9:end -length(PC_Coff)-9));
end

对匹配滤波的结果进行评估

$\begin{array}{c} SNR_1 = -5dB \\ SNR_2 = 3dB\\ SNR_{1_{out}} = 28.37dB\\ SNR_{2_{out}} = 32.15dB\\ \end{array}$

MTI与MTD

对匹配滤波后的矩阵进行一次对消

%% MTI
for m=1:1:M-1
    MTI_data(m,:) = PC_data(m+1,:) - PC_data(m,:);
end
figure
mesh(abs(MTI_data));

对MTI的矩阵进行如下处理

%% MTD
for l = 1:1:length(MTI_data(1,:))
    MTD_data(:,l) =fftshift( fft(MTI_data(:,l)));  %对每一列FFT（相参积累）
end
figure
mesh(abs(MTD_data));

相参积累

%% 相参积累

for l = 1:1:length(PC_data(1,:))
    PC_data_CA(:,l) =fftshift( fft(PC_data(:,l)));  %对每一列FFT（相参积累）
end

figure
x =(1:length(PC_data_CA(1,:))) *c/10e6/2;
y = (-round( length(PC_data_CA(:,1))/2  ):1:round( length(PC_data_CA(:,1))/2 )-1 ) *lambda/( 2*T*length(PC_data_CA(:,1)) ); 
mesh(x,y ,abs(PC_data_CA));
title('相参处理结果');
xlabel('距离');ylabel('速度');
set(gca,'Ydir','reverse');

经过数字下变频，匹配滤波，相参处理后得到如下结果。

一个匹配滤波小实验

使用一单频连续波测速雷达，沿垂直其主瓣照射方向匀速推动，示意图如下：

实际雷达照射面下的物体如下：

IData =  csvread('Q6.csv');
QData =  csvread('I6.csv');

IData = IData(:,2);
QData = QData(:,2);

EchoData = QData + 1i*IData;
EchoData = EchoData(1:10:70000);
sizeEchoData = size(EchoData);
EchoData = reshape(EchoData,[1,sizeEchoData(1)]);

load('D:\Matlab2018a\SpeedDetect\GaussianWin_Point256_Alpha2_5.mat');
WinLength = length(GaussianWin_Point256_Alpha2_5);
Step = 20;
tEchoData = (1/25000 :1/25000 :7000*1/25000);
figure
subplot(2,1,1);
plot(tEchoData,real(EchoData));xlabel('时间（s）');ylabel('幅值（V）');title('时域波形（实）');
subplot(2,1,2);
plot(tEchoData,imag(EchoData));xlabel('时间（s）');ylabel('幅值（V）');title('时域波形（虚）');

result=STFT(EchoData,GaussianWin_Point256_Alpha2_5,WinLength,Step);

Fs = 2.5e3;
sizeResult = size(result);
t = 1/Fs*Step:1/Fs*Step:sizeResult(1)*1/Fs*Step;
v = -(WinLength-1)/2*Fs/WinLength/161 : Fs/WinLength/161 :  (WinLength-1)/2*Fs/WinLength/161;
figure
imagesc(v,t,abs(result));ylabel('时间（s）');xlabel('速度（m/s）');title('短时傅里叶分析结果');

Fs = 2.5e3;
angle_max = 10/360*2*pi;
h = 1.21;
d = tan(angle_max)*h;
va = 1.15;%2.34

t_total = d*2/va;
t = 0:1/Fs:t_total;

angle_now = atan( ( d*ones(1,length(t))- va*t)/h );
v_alpha = va * sin(angle_now);

fc = 24.15e9;
c = 3e8;

desire_signal = exp(1i*v_alpha*2*fc/c);
result = xcorr(EchoData,conj(desire_signal));
result = abs(result(6000:length(result)));

figure
imagesc(abs(result));ylabel('能量维');xlabel('时间维');title('脉冲压缩');
figure
plot(abs(result));ylabel('能量维');xlabel('时间维');title('脉冲压缩');

实际回波的波形为

短时傅里叶分析结果为

脉冲压缩的结果为

目标跟踪中波门形状与参数

环形波门

椭圆（球）波门

MN逻辑法航迹起始

仿真代码

原理简述

仿真结果

13位Barker码二进制相位调制波形仿真

LFM信号仿真

交互多模型

滤波模型

某一模型的状态的预测概率密度和预测的模型概率

似然函数

归一化因数

条件概率密度和条件模型概率

IMM迭代计算方程

仿真

不敏卡尔曼滤波

不敏变换（UT）

Choose Sigma Points

不敏卡尔曼滤波算法

卡尔曼滤波

假设条件

高斯分布与高斯乘积定理

卡尔曼迭代

预测函数

似然函数与归一化因子

后验概率密度函数

算法流程

matlab仿真

贝叶斯推理

贝叶斯定理

目标跟踪中的贝叶斯递推

非机动目标跟踪与最优滤波

目标跟踪中的最优贝叶斯滤波

最优非机动目标跟踪滤波

雷达信号处理基基础

脉冲体制

回波信号分析

匹配滤波原理简述

仿真

参数设计

回波生成

数字正交下变频（DDC）

MTI与MTD

相参积累

一个匹配滤波小实验

连续波体制