JPDA的基本模型
确认矩阵
比如有这样一个情况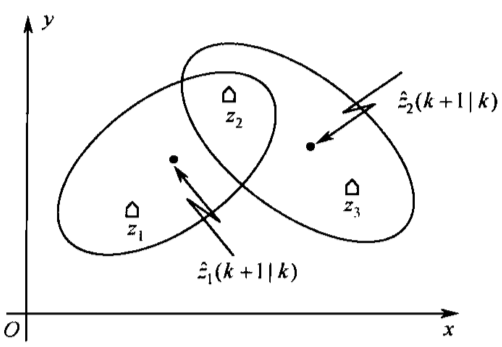
那么根据规则可以建立确认矩阵
互联矩阵(联合事件)
联合事件与互联矩阵一一对应
所谓互联矩阵,用之前的例子举例就是将$\Omega$拆分成
互联概率的计算
符号定义:
$\theta_i(k)$:表示第 $i$ 个联合事件
$\hat{\Omega}\left[\theta_{i}(k)\right]$:表示与第 $i$ 个联合事件对应的互联矩阵
根据上述两个基本假设容易推出互联矩阵满足:
用文字叙述就是:
每一个量测只来源于一个目标或者是杂波虚警
每一个目标只有一个或者没有量测$\theta_{jt}(k)$:测量 $j$ 源于目标 $t(1\leq t \leq T)$ 的事件,$\theta_{0t}$ 表示目标是杂波或者虚警
$\beta_{jt}(k)$:表示第 $j$ 个测量与 $t$ 互联的概率,且
$\theta_{j t}^{i}(k)$:量测 $j$ 在第 $i$ 个联合事件中源于目标 $t(0 \leqslant t \leqslant T)$ 的事件
$\hat{\omega}_{j t}^{i}\left(\theta_{i}(k)\right)$:表示在第 i 个联合事件中,量测 j 是否源于目标 $t,$ 在量测 j 源于目标 $t$ 时为 $1,$ 否则为 0
状态估计计算
则 $k$ 时刻目标 $t$ 的状态估计为
式中
表示在 $k$ 时刻用第 $j$ 个量测对目标 $t$ 进行卡尔曼滤波所得的状态估计。
$\hat{\boldsymbol{X}}_{0}^{t}(k \mid k)$ 表示 $k$时刻没有量测源于目标的情况,这时需要用预测值 $\hat{\boldsymbol{X}}^{t}(k \mid k-1)$ 来代替,即:
概率计算
第 $j$ 个量测与目标互联的概率可利用下式求取:
可以看到求取状态估计 $\hat{\boldsymbol{X}}^{t}(k \mid k)$ 的关键就是计算联合事件概率(后验条件概率) $\operatorname{Pr}\left\{\theta_{i}(k) \mid Z^{k}\right\}$
联合事件概率计算
为了以后讨论问题的方便,这里引入两个二元指示变量:
(1) 量测互联指示,即
表示量测 j 在联合事件 $\theta_{i}(k)$ 中是否跟一个真实目标互联:
(2) 目标检测指示,即
表示任一量测在联合事件 $\theta_{i}(k)$ 中是否与目标 $t$ 互联,也即目标 $t$ 是否被检测。
设 $\phi\left[\theta_{i}(k)\right]$ 表示在联合事件 $\theta_{i}(k)$ 中假量测的数量,则
核心问题:求解 $\operatorname{Pr}\left\{\theta_{i}(k) \mid Z^{k}\right\}$
一看这形式老朋友了,贝叶斯推论三步走起
式中,c 为归一化常数
似然函数:
其中
联合事件 $\theta_{i}(k)$ 的先验概率:
其中
最后得到
状态估计协方差计算
没有测量来自目标
有测量来自目标
算法仿真
在航迹起始的基础上进行仿真1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140clc
clear all
close all
load('Root.mat');
load('points.mat');
points = points(11:end);
n = size(points,1);
n_z = 2;
gamma = chi2inv(0.99,n_z);
P_G = PG(gamma,n_z);
T = 1;
F = [1 0 T 0;
0 1 0 T;
0 0 1 0;
0 0 0 1];
H = [1 0 0 0;
0 1 0 0];
Gamma=[T*T/2 0;0 T*T/2;T 0;0 T];
Q = 0.01*Gamma*Gamma';%根据实际过程噪声的协方差更改
R = 5*H*H'; %根据实际测量误差的协方差更改
for kk =1:n
Z_k = cell2mat(points(kk));
t = size(Root,2); % 目标数
mk = size(Z_k,2); %有效测量数
for i = 1:t
P(:,:,i)=F*Root(i).pkk*F'+Q;
S(:,:,i) = H*P(:,:,i)*H' + R;
K(:,:,i)= P(:,:,i)*H'*inv(S(:,:,i));
Z_predict(:,i) = H*Root(i).x_predict;
Volume(i)=ellipse_Volume(gamma,n_z,S(:,:,i));
end
%% 建立确认矩阵
Omega = zeros(mk,t+1);%确认矩阵
Z_set = [];
for j = 1:t
for k = 1:mk
V=(Z_k(:,k)-Z_predict(:,j))'*inv(S(:,:,j))*(Z_k(:,k)-Z_predict(:,j));
if (V<=gamma)
Omega(k,1) = 1;
Omega(k,j+1) = 1;
Z_set = [Z_set k]; % 记录确认矩阵对应的量测 索引
end
end
end
Z_set = unique(Z_set,'stable');
Omega(all(Omega==0,2),:)=[]; %删除确认矩阵的零行
%% 建立互联矩阵
hat_omega=zeros(size(Omega,1),size(Omega,2),10000);
hat_omega(:,1,1:10000)=1;
num=1;
for i=1:size(Omega,1)
if Omega(i,2)==1
hat_omega(i,2,num)=1;hat_omega(i,1,num)=0;
num=num+1;
for j=1:size(Omega,1)
if (i~=j)&&(Omega(j,3)==1)
hat_omega(i,2,num)=1;hat_omega(i,1,num)=0;
hat_omega(j,3,num)=1;hat_omega(j,1,num)=0;
num=num+1;
for k=1:size(Omega,1)
if (k~=i)&&(k~=j)&&(Omega(k,4)==1)
hat_omega(i,2,num)=1;hat_omega(i,1,num)=0;
hat_omega(j,3,num)=1;hat_omega(j,1,num)=0;
hat_omega(k,4,num)=1;hat_omega(k,1,num)=0;
num=num+1;
end
end
end
end
end
end
hat_omega=hat_omega(:,:,1:num);
%% 计算theta_i 条件概率
P_D = 0.5;
Pr = PrthetaZk(hat_omega,t,Z_k,Z_set,Z_predict,S,P_D,sum(Volume));
%% 计算互联概率 beta
beta = zeros(length(Z_set)+1,t);
for i=1:t
for j=1:length(Z_set)
for k=1:num
beta(j+1,i)=beta(j+1,i)+Pr(k)*hat_omega(j,i+1,k);
end
end
end
% 计算j = 0的特殊情况,同时满足归一化
beta(1,:) = 1-sum(beta(2:end,:));
%% 计算状态估计X_jt
X_jt = cell(length(Z_set)+1,t);
% 计算j = 0的特殊情况
for i = 1:t
X_jt(1,i) = {Root(i).x_predict};
end
for i = 1:t
for j = 2:length(Z_set)+1
X_jt(j,i) = {Root(i).x_predict + K(:,:,i)*(Z_k(:,Z_set(j-1)) - Z_predict(:,i))};
end
end
X_t = zeros(size(Root(1).x_predict,1),t);
temp = zeros([size(Root(1).pkk) t]);
for i = 1:t
%% 计算状态估计X_t
for j = 1:length(Z_set)+1
X_t(:,i) = X_t(:,i) + beta(j,i)*X_jt{j,i};
temp(:,:,i) = temp(:,:,i) +beta(j,i)*X_jt{j,i}*X_jt{j,i}';
end
%% 计算后验协方差
Root(i).pkk = P(:,:,i) - (1-beta(1,i))*K(:,:,i)*S(:,:,i)*K(:,:,i)'+temp(:,:,i)-X_t(:,i)*X_t(:,i)';
Root(i).seq =[Root(i).seq X_t(1:2,i)];
Root(i).est =[Root(i).est X_t(:,i)];
Root(i).x_predict = F*X_t(:,i);
end
end
figure
hold on
for j = 1:n
Z = cell2mat(points(j));
plot(Z(1,:),Z(2,:),'.r');
end
for i = 1:t
Root(i).show;
end
xlabel('x轴坐标(m)');
ylabel('y轴坐标(m)');
title('JPDA数据关联');
运行结果如下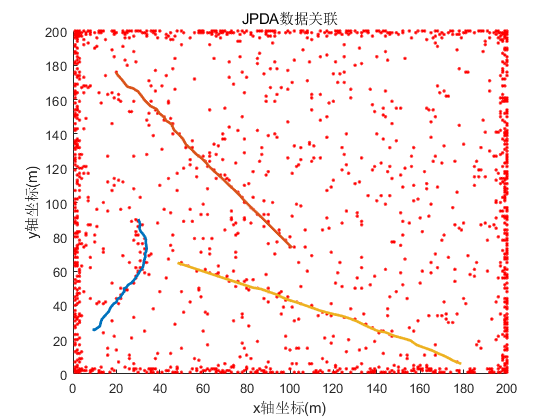
JPDA的公式描述看似繁琐但是其实多是在进行二进制的判定,核心仍然是贝叶斯递推,接下来就带着大家进行公式向matlab代码的翻译过程:
首先先简单描述一下代码实现的流程,我尽量用白话和公式各描述一遍,在获得了某一量测的时间点:
语言描述:
- 根据上一时刻状态估计协方差进行状态预测协方差以及新息协方差计算,以及测量值的预测值计算
- 根据有效的量测以及目标建立确认矩阵
- 根据规则对确认矩阵分解为联合事件对应的互联矩阵
- 计算每一种联合事件的发生概率
- 根据联合事件发生概率计算量测与目标互联的概率
- 计算当前时点的目标状态估计
- 计算目标状态估计的协方差
公式描述:(这里使用线性的贝叶斯迭代也就是kalmanfilter) - 式中即