MN逻辑法航迹起始
设 $z_{i}^{l}(k)$ 是 $k$ 时刻量测 $i$ 的第 $l$ 个分量, 这里 $l=1, \cdots, p, \quad i=1, \cdots, m_{k}, \quad$ 则可将观测值
$\boldsymbol{Z}_{i}(k)$ 与 $\boldsymbol{Z}_{j}(k+1)$ 间的距离矢量 $\boldsymbol{d}_{i j}$ 的第 $l$ 个分量定义为
式中, $T$ 为两次扫描问的时间问隔。若假设观测误差是独立、零均值、高斯分布的, 方差为 $\boldsymbol{R}_{i}(k), \quad$ 则归一化距离平方为
式中, $D_{i j}(k)$ 为服从自由度为 $p$ 的 $\chi^{2}$ 分布的随机变量。由给定的门限概率查自由度 $p$ 为 $\chi^{2}$ 分布武可得门限 $\gamma, \quad$ 若 $D_{i j}(k) \leqslant \gamma,$ 则可判定 $Z_{i}(k)$ 和 $\boldsymbol{Z}_{\boldsymbol{j}}(k+1)$ 两个量测互联。
仿真代码
首先为了方便后续代码管理定义航迹的类1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18classdef Track
properties
start = [];
seq = [];
est = [];
pkk = [];
x_predict = [];
end
methods
function obj = Track(Z)
obj.start = Z;
obj.seq = Z;
end
function show(obj)
plot(obj.est(1,:),obj.est(2,:),'linewidth',2);
end
end
end
接下来就是实现航迹起始的函数:
采用线性贝叶斯迭代方法进行外推与波门大小的估计
航迹起始采用逻辑法的判别
后续的外推判决采用最邻近滤波(NN)方法1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139function [Root] = MNStarter(points,N,M,vmin,vmax)
% points 是为N次量测的集合
% N 如上
% M 航迹确认的门限
% vmin 速度最小值 用于初始化的圆(球)波门
% vmax 速度最大值 用于初始化的圆(球)波门
% Root 返回值为Track类的变量
T = 1;
threshold = chi2inv(0.8,2);
track = {};
F = [1 0 T 0;
0 1 0 T;
0 0 1 0;
0 0 0 1];
H = [1 0 0 0;
0 1 0 0];
Gamma=[T*T/2 0;0 T*T/2;T 0;0 T];
Q = Gamma*Gamma'*0.1;%根据实际过程噪声的协方差更改
R = 5*H*H'; %根据实际测量误差的协方差更改
pair = {};
outside = [];
set = [];
index = 1;
Z_k = cell2mat(points(1));
Z_k_plus1 = cell2mat(points(2));
for j = 1:size(cell2mat(points(1)),2)
for k = 1:size(cell2mat(points(2)),2)
d = max(0,norm(Z_k_plus1(:,k)-Z_k(:,j))-vmax*T)+max(0,-norm(Z_k_plus1(:,k)-Z_k(:,j))+vmin*T);
D = d'*(R+R)^-1*d;
if D <= threshold
pair = [pair ;[Z_k(:,j),Z_k_plus1(:,k)]];
% 初始化协方差
Px0 = 5*eye(4);
P=F*Px0*F'+Q;%预测协方差阵
S(:,:,index)=H*P*H'+R;%计算新息协方差
K = P*H'*inv(S(:,:,index));
Pkk(:,:,index) = (eye(4)-K*H)*P;%计算后验方差
%计算由前两次量测组成的直线进行外推
x_init=[Z_k_plus1(:,k);(Z_k_plus1(:,k)-Z_k(:,j))/T];%利用前两个观测值来对初始条件进行估计
x_forest(:,index)=F*x_init;%状态的一步预测
out_forest=H*x_forest(:,index);%观测的一步预测
outside=[outside out_forest];%外推点
index = index +1;
end
end
end
board = zeros(1,size(pair,1)); %计分板
for j=3:N
Z_k = cell2mat(points(j));
for t=1:index-1
P=F*Pkk(:,:,t)*F'+Q;
SS = H*P*H' + R;
K = P*H'*inv(SS);
for i=1:(size(Z_k,2))
%计算后续的扫描点落在外推点跟踪门内的系数
V(i)=(Z_k(:,i)-outside(:,t))'*inv(SS)*(Z_k(:,i)-outside(:,t));
end
[key dex]=min(V);
%判断是否有回波落入到门波之内,有则取离外推点最近的给予互联
if (key<=threshold)
% x_init=[Z_k(:,dex);(Z_k(:,dex)-pair{t}(:,end))/T];
% pair(t,:)={[pair{t} Z_k(:,dex)]};
% x_forest=F*x_init;
% outside(:,t)=H*x_forest;
pair(t,:)={[pair{t} Z_k(:,dex)]};
x_est = x_forest(:,t) + K*(Z_k(:,dex)-outside(:,t));
Pkk(:,:,t) = (eye(4)-K*H)*P;
x_forest(:,t)=F*x_est;
outside(:,t)=H*x_forest(:,t);
else
pair(t,:)={[pair{t} outside(:,t)]};
Pkk(:,:,t) = P;
x_forest(:,t)=F*x_forest(:,t);
outside(:,t)=H*x_forest(:,t);
board(t) = board(t)+1;
end
end
V=[];
end
% icon=['*','+','o','s','d','.'];
% figure
% hold on
% for i = 1:N
% Z = cell2mat(points(i));
% plot(Z(1,:),Z(2,:),icon(mod(i,6)+1));
% end
num_trace = 0 ;
index = 1;
for i = 1:size(pair,1)
trace = cell2mat(pair(i));
if N-board(i) >= M
% plot(trace(1,:),trace(2,:),'pk');
% plot(trace(1,:),trace(2,:),'-');
% pause(0.5);
Root(index) = Track(trace(:,1));
Root(index).seq = trace;
index = index +1;
num_trace = num_trace + 1;
end
end
for i = 1:num_trace
xe = [];
xe(:,1) =[ Root(i).start;zeros(2,1)];
P = eye(4);
for j = 2:size(Root(i).seq,2)
[xe(:,j),P] = KalmanFilter(Root(i).seq(:,j),xe(:,j-1),F,H,P,Q,R);
end
Root(i).pkk = P;
Root(i).est = xe;
Root(i).x_predict = F*xe(:,j);
% plot(xe(1,:),xe(2,:),'linewidth',2);
end
% figure
% hold on
% for i = 1:num_trace
% Root(i).show;
% end
end
接下来给出一个测试的代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19clc;close all;clear all
load('points_prev.mat');
N = 8;
M = N * 3 /4;
vmin = 0.5;
vmax = 4;
[Root] = MNStarter(points,N,M,vmin,vmax);
figure
hold on
for i = 1:size(Root,2)
Root(i).show;
end
xlabel('x轴坐标(m)');
ylabel('y轴坐标(m)');
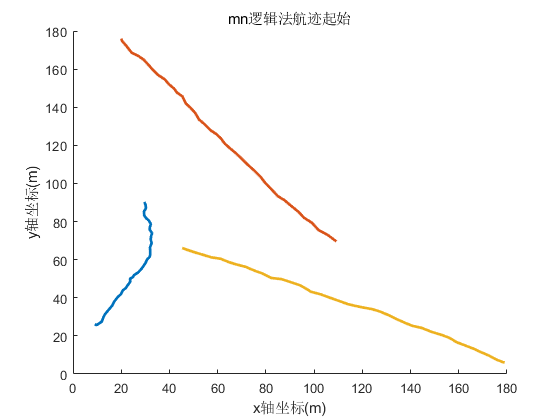
title('mn逻辑法航迹起始');
运行可以得到: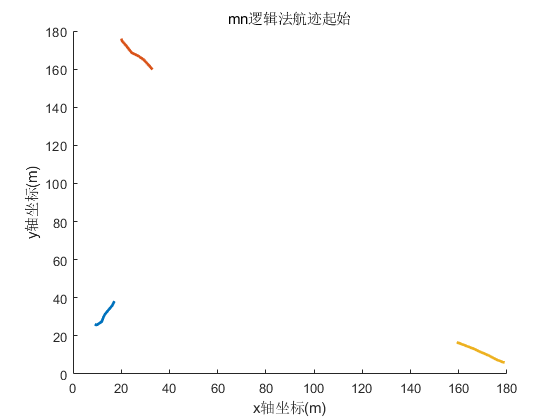
如果多个目标距离较远,并且虚警率较低那么通过NN方法就可以经进行航迹的绘制
将上面的测试代码N更改为40