原理简述
采用自适应滤波器设计中的递归最小二乘(RLS)方法,通过合理安排输入信号与期望信号的结构来设计脉冲压缩雷达数字旁瓣抑制滤波器,具有算法简单实用,适用广泛的特点,可用于线性调频、二相码和多相码等各种信号。在滤波器抽头有限的情况下,峰值旁瓣电平低于-40dB。主瓣宽度仅为单位采样符号间隔。
衡量旁瓣抑制滤波器性能的指标主要有峰值旁瓣电平(PSL,peak side lobe level)和积累旁瓣电平(ISL,integrated side lobe level),它们分别定义为最大旁瓣功率与峰值响应的比值以及旁瓣总功率与峰值响应的比值。
对于雷达来说,理想的匹配滤波压缩波形应为一$\delta$函数。在实际的脉压波形中,非零旁瓣可视为噪声,于是,旁瓣抑制过程可看作是自适应噪声对消,只不过输入为原始的压缩信号(匹配滤波输出)。下图表示出了在迭代训练时,这种横向滤波器的结构框图。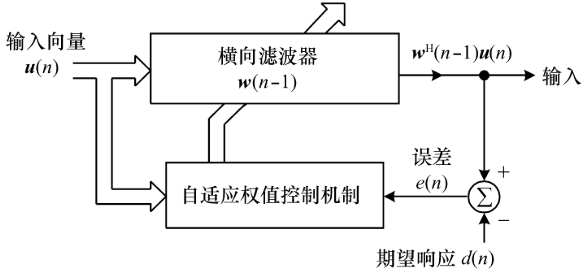
若设$\boldsymbol{x}$为$f_s(t)$的匹配滤波输出包络 , 则迭代时,输入信号$\boldsymbol{u}$应为$\boldsymbol{x}$的重复。为了消除前后$\boldsymbol{x}$之间的影响 ,其间应插入零向量$\boldsymbol{z}$, 且$\boldsymbol{z}$的长度应至少为所设定 的滤波器长度。这样才能使信号$\boldsymbol{x}$全部移出滤波器 后 ,下一个$\boldsymbol{x}$才进入滤波器;同时为了减少迭代次数, 零向量的长度又不宜过长。故$\boldsymbol{u}$为
且有关系
式中, $L_w$为滤波器抽头长度;$L_z$为零向量 z的长度。
期望响应$\boldsymbol{d}$为理想狄拉克信号$\delta$的周期重复
考虑到FIR滤波器的时延特性那么,在$\delta$中,1的位置在$(L_w+L_x)/{2}$。
之后根据RLS迭代算法
初始化条件:
其中$\rho$为正则化参数,其设定与信噪有关, 高信噪比时取较小值,低信噪比时取较大值。
仿真结果
13位Barker码二进制相位调制波形仿真
13位巴克码码元为$[1,1 ,1, 1, 1, -1 ,-1 ,1 ,1 ,-1 ,1 ,-1, 1 ]$
通过匹配滤波器的结果如图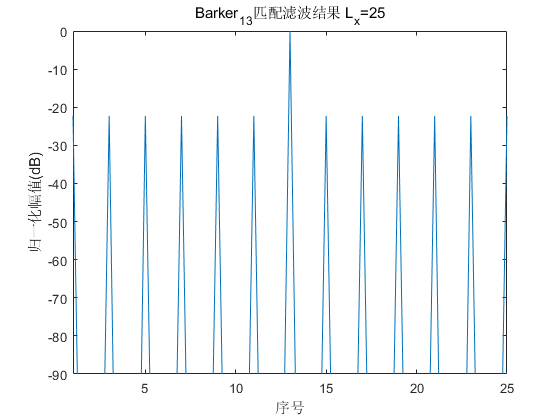
经过RS-RLS自适应滤波设计滤波器系数后得到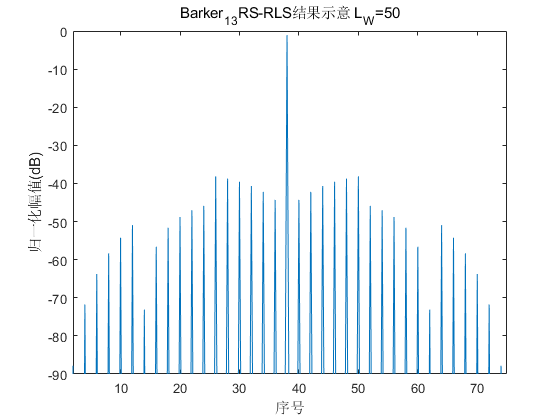
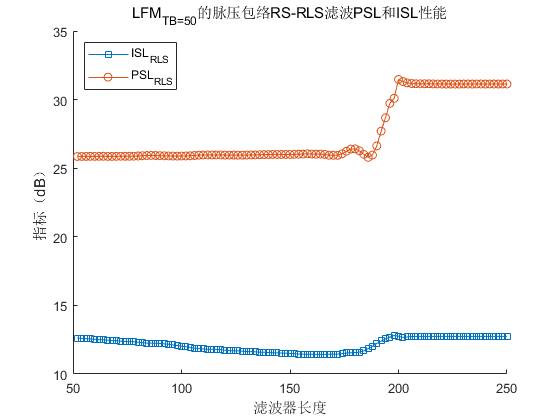
通过对不同长度的滤波器进行PSL和ISL指标进行仿真得到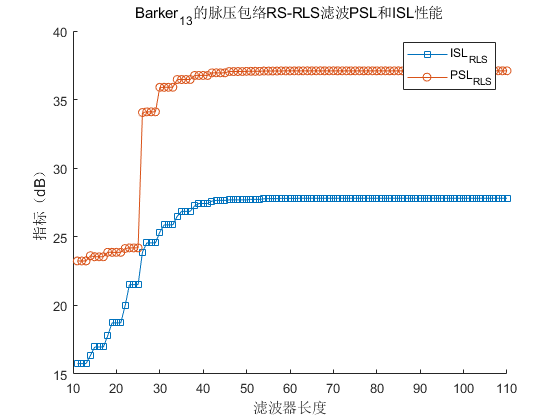
LFM信号仿真
通过匹配滤波器的结果如图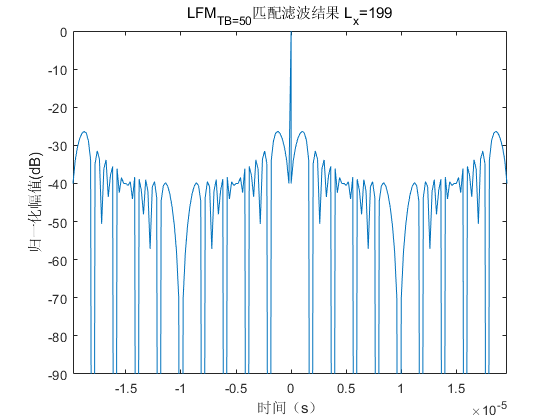
经过RS-RLS自适应滤波设计滤波器系数后得到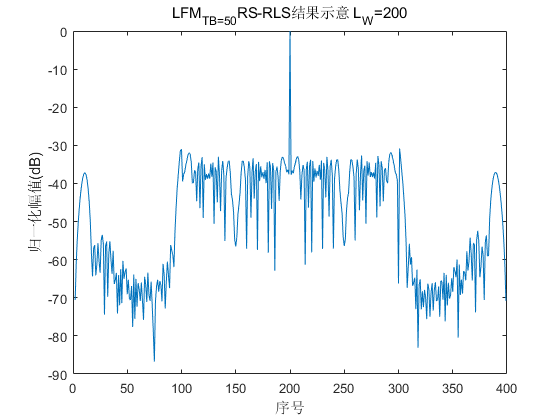
通过对不同长度的滤波器进行PSL和ISL指标进行仿真得到