IMMKF

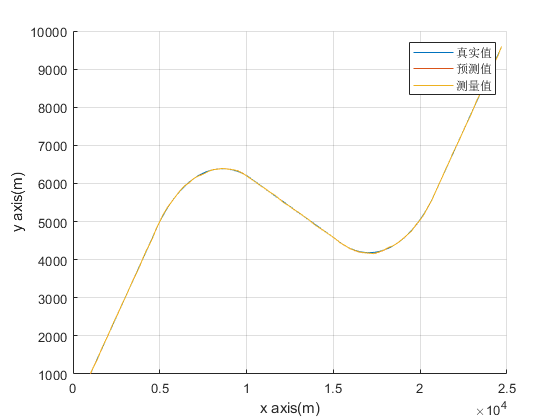
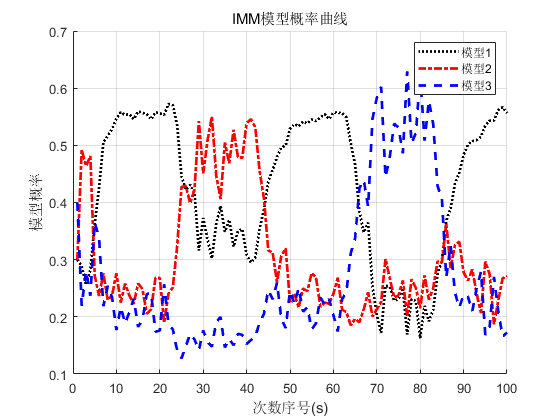
交互多模型

滤波模型

假定目标动态特性包含在以下模型集中：

$$\boldsymbol{x}_{k}=\boldsymbol{f}_{r_{k}}\left(\boldsymbol{x}_{k-1}, \boldsymbol{u}_{k}\right)+\boldsymbol{v}_{r_{k}}, \quad r_{k} \in\{1,2, \cdots, d\}$$

$r_{k}$ 是在状态空间内 $\{1,2, \cdots, d\}$ 满足一致性离散马尔可夫链的随机变量。

目标状态的后验概率密度 $p\left(\boldsymbol{x}_{k} \mid \boldsymbol{y}^{k}\right)$ 通过对联合概率密度各分量求和得

$$p\left(\boldsymbol{x}_{k} \mid \boldsymbol{y}^{k}\right)=\sum_{i=1}^{d} p\left(\boldsymbol{x}_{k}, r_{k}=i \mid \boldsymbol{y}^{k}\right)$$

利用条件概率引理，上述方程右侧的联合概率密度可以分解为两项之积，即

$$p\left(\boldsymbol{x}_{k}, r_{k}=i \mid \boldsymbol{y}^{k}\right)=p\left(\boldsymbol{x}_{k} \mid r_{k}=i, \boldsymbol{y}^{k}\right) p\left(r_{k}=i \mid \boldsymbol{y}^{k}\right)$$

令 $\mu_{k \mid k}(i)=p\left(r_{k}=i \mid \boldsymbol{y}^{k}\right),$ 后验概率密度可以表示为

$$p\left(\boldsymbol{x}_{k} \mid \boldsymbol{y}^{k}\right)=\sum_{i=1}^{d} p\left(\boldsymbol{x}_{k} \mid r_{k}=i, \boldsymbol{y}^{k}\right) \mu_{k \mid k}(i)$$

将 $\boldsymbol{y}^{k}$ 展开为 $\left\{\boldsymbol{y}_{k}, \boldsymbol{y}^{k-1}\right\}$,利用贝叶斯理论可以得到上述方程右侧求和第一项的递推式:

$$\begin{aligned} p\left(\boldsymbol{x}_{k} \mid r_{k}=i, \boldsymbol{y}^{k}\right) &=p\left(\boldsymbol{x}_{k} \mid r_{k}=i, \boldsymbol{y}_{k}, \boldsymbol{y}^{k-1}\right) \\ &=\frac{p\left(\boldsymbol{y}_{k} \mid \boldsymbol{x}_{k}, r_{k}=i, \boldsymbol{y}^{k-1}\right)}{p\left(\boldsymbol{y}_{k} \mid r_{k}=i, \boldsymbol{y}^{k-1}\right)} p\left(\boldsymbol{x}_{k} \mid r_{k}=i, \boldsymbol{y}^{k-1}\right) \end{aligned}$$

式中: $p\left(\boldsymbol{x}_{k} \mid r_{k}=i, \boldsymbol{y}^{k-1}\right)$ 为预测概率密度 $; p\left(\boldsymbol{y}_{k} \mid \boldsymbol{x}_{k}, r_{k}=i, \boldsymbol{y}^{k-1}\right)$ 为似然函数 ; $p(\boldsymbol{y}_{k} \mid r_{k}=i, \boldsymbol{y}^{k-1}$ ) 为归一化因子。 式(3.45)的求和分量第二项 $\mu_{k \mid k}(i)=p\left(r_{k}=i \mid \boldsymbol{y}^{k}\right)$ 也可以通过递推计算。同 样将 $\boldsymbol{y}^{k}$ 展开为 $\left\{\boldsymbol{y}_{k}, \boldsymbol{y}^{k-1}\right\},$ 利用贝叶斯理论可得

$$\begin{aligned} \mu_{k \mid k}(i)=p\left(r_{k}=i \mid \boldsymbol{y}_{k}, \boldsymbol{y}^{k-1}\right)=\frac{p\left(\boldsymbol{y}_{k} \mid r_{k}=i, \boldsymbol{y}^{k-1}\right) p\left(r_{k}=i \mid \boldsymbol{y}^{k-1}\right)}{p\left(\boldsymbol{y}_{k} \mid \boldsymbol{y}^{k-1}\right)} \end{aligned}$$

令 $p\left(r_{k}=i \mid \mathbf{y}^{k-1}\right)=\boldsymbol{\mu}_{k \mid k-1}(i),$ 条件模型概率可表示为

$$\begin{aligned} \mu_{k \mid k}(i)=\frac{p\left(\boldsymbol{y}_{k} \mid r_{k}=i, \boldsymbol{y}^{k-1}\right) \mu_{k \mid k-1}(i)}{p\left(\boldsymbol{y}_{k} \mid \boldsymbol{y}^{k-1}\right)} \end{aligned}$$

式中: $\mu_{k \mid k-1}(i)$ 为模型预测概率 $; p\left(\boldsymbol{y}_{k} \mid r_{k}=i, \boldsymbol{y}^{k-1}\right)$ 为似然函数 $; p\left(\boldsymbol{y}_{k} \mid \boldsymbol{y}^{k-1}\right)$ 为归一
化因子。

某一模型的状态的预测概率密度和预测的模型概率

$$\begin{aligned} p\left(\boldsymbol{x}_{k} \mid r_{k}=i, \boldsymbol{y}^{k-1}\right) &=\int_{\boldsymbol{x}_{k-1}} p\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{k-1}, r_{k}=i, \boldsymbol{y}^{k-1}\right) \sum_{j=1}^{d} p\left(\boldsymbol{x}_{k-1} \mid r_{k-1}\right.\\ &\left.=j, \boldsymbol{y}^{k-1}\right) \mu_{k-11 k}^{j i} \mathrm{d} \boldsymbol{x}_{k-1} \\ &=\int_{\boldsymbol{x}_{k-1}} N\left(\boldsymbol{x}_{k} ; \boldsymbol{F}_{i} \boldsymbol{x}_{k-1}+\boldsymbol{u}_{i}, \boldsymbol{Q}_{i}\right) N\left(\boldsymbol{x}_{k-1} ; \hat{\boldsymbol{x}}_{k-1 \mid k-1}^{0 i}, \boldsymbol{P}_{k-1 \mid k-1}^{0 i}\right) \mathrm{d} \boldsymbol{x}_{k-1} \\ &=N\left(\boldsymbol{x}_{k} ; \hat{\boldsymbol{x}}_{k \mid k-1}^{i}, \boldsymbol{P}_{k \mid k-1}^{i}\right) \end{aligned}$$

其中，均值和协方差分别为

$$\begin{aligned} \hat{\boldsymbol{x}}_{k \mid k-1}^{i} =\boldsymbol{F}_{\boldsymbol{i}} \hat{\boldsymbol{x}}_{k-1 \mid k-1}^{0 i}+\boldsymbol{u}_{i} \\ \boldsymbol{P}_{k \mid k-1}^{i}= \boldsymbol{F}_{i} \boldsymbol{P}_{k-1 \mid k-1}^{0 i} \boldsymbol{F}_{i}^{\mathrm{T}}+\boldsymbol{Q}_{i} \end{aligned}$$

预测模型概率 $\mu_{k \mid k-1}(i)$ 可以展开为

$$\begin{aligned} \mu_{k \mid k-1}(i) &=p\left(r_{k}=i \mid \boldsymbol{y}^{k-1}\right) \\ &=\sum_{j=1}^{d} p\left(r_{k}=i \mid r_{k-1}=j, \boldsymbol{y}^{k-1}\right) p\left(r_{k-1}=j \mid \boldsymbol{y}^{k-1}\right) \\ &=\sum_{j=1}^{d} \Gamma_{j i} p\left(r_{k-1}=j \mid \boldsymbol{y}^{k-1}\right) \\ &=\sum_{j=1}^{d} \Gamma_{j i} \mu_{k-1 \mid k-1}(j) \end{aligned}$$

似然函数

$$p\left(\boldsymbol{y}_{k} \mid \boldsymbol{x}_{k}, r_{k}=i, \boldsymbol{y}^{k-1}\right)=p\left(\boldsymbol{y}_{k} \mid \boldsymbol{x}_{k}\right)=N\left(\boldsymbol{y}_{k} ; \boldsymbol{H} \boldsymbol{x}_{k}, \boldsymbol{R}_{k}\right)$$

令$\lambda_{k}(i)=p\left(\boldsymbol{y}_{k} \mid r_{k}=i, \boldsymbol{y}^{k-1}\right)$则 $\lambda_{k}(i)=N\left(\boldsymbol{y}_{k} ; \boldsymbol{H} \hat{\boldsymbol{x}}_{k-1 \mid k-1}^{i}, \boldsymbol{H} \boldsymbol{P}_{k \mid k-1}^{i} \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{R}_{k}\right)$

归一化因数

$$\begin{aligned} p\left(\boldsymbol{y}_{k} \mid \boldsymbol{y}^{k-1}\right) &=\sum_{i=1}^{d} p\left(\boldsymbol{y}_{k} \mid r_{k}=i, \boldsymbol{y}^{k-1}\right) p\left(r_{k}=i \mid \boldsymbol{y}^{k-1}\right) \\ &=\sum_{i=1}^{d} \lambda_{k}(i) \sum_{j=1}^{d} \Gamma_{j i} \mu_{k-1 \mid k-1}(j) \end{aligned}$$

条件概率密度和条件模型概率

条件概率密度展开为

$$\begin{aligned} p\left(\boldsymbol{x}_{k} \mid r_{k}=i, \boldsymbol{y}^{k}\right) &=\frac{p\left(\boldsymbol{y}_{k} \mid \boldsymbol{x}_{k}, r_{k}=i, \boldsymbol{y}^{k-1}\right) p\left(\boldsymbol{x}_{k} \mid r_{k}=i, \mathbf{y}^{k-1}\right)}{p\left(\boldsymbol{y}_{k} \mid r_{k}=i, \mathbf{y}^{k-1}\right)} \\ &=\frac{N\left(\boldsymbol{y}_{k} ; \boldsymbol{H} \boldsymbol{x}_{k}, \boldsymbol{R}_{k}\right) N\left(\boldsymbol{x}_{k} ; \hat{\boldsymbol{x}}_{k \mid k-1}^{i}, \boldsymbol{P}_{k \mid k-1}^{i}\right)}{N\left(\boldsymbol{y}_{k} ; \boldsymbol{H} \hat{\boldsymbol{x}}_{k \mid k-1}^{i}, \boldsymbol{H} \boldsymbol{P}_{k \mid k-1}^{i} \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{R}_{k}\right)} \end{aligned}$$

条件概率密度可以近似为高斯分布, 即 $p\left(\boldsymbol{x}_{k} \mid r_{k}=i, \boldsymbol{y}^{k}\right)=N\left(\boldsymbol{x}_{k} ; \hat{\boldsymbol{x}}_{k \mid k}^{i}, \boldsymbol{P}_{k \mid k}^{i}\right),$ 其
均值和协方差为

$$\begin{aligned} \hat{\boldsymbol{x}}_{k \mid k}^{i}=\hat{\boldsymbol{x}}_{k \mid k-1}^{i}+\boldsymbol{P}_{k \mid k-1}^{i} \boldsymbol{H}^{\mathrm{T}}\left(\boldsymbol{H} \boldsymbol{P}_{k \mid k-1}^{i} \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{R}_{k}\right)^{-1}\left(\boldsymbol{y}_{k}-\boldsymbol{H} \hat{\boldsymbol{x}}_{k \mid k-1}^{i}\right) \\ \boldsymbol{P}_{k \mid k}^{i}=\boldsymbol{P}_{k \mid k-1}^{i}-\boldsymbol{P}_{k \mid k-1}^{i} \boldsymbol{H}^{\mathrm{T}}\left(\boldsymbol{H} \boldsymbol{P}_{k \mid k-1}^{i} \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{R}_{k}\right)^{-1} \boldsymbol{H} \boldsymbol{P}_{k \mid k-1}^{i} \end{aligned}$$

条件模型概率 $p\left(r_{k}=i \mid \boldsymbol{y}^{k}\right)$ 为

$$\begin{aligned} \mu_{k \mid k}(i)=\frac{p\left(\boldsymbol{y}_{k} \mid r_{k}=i, \boldsymbol{y}^{k-1}\right) p\left(r_{k}=i \mid \boldsymbol{y}^{k-1}\right)}{p\left(\boldsymbol{y}_{k} \mid \boldsymbol{y}^{k-1}\right)} \end{aligned}$$

经简化可得

$$\begin{aligned} \mu_{k \mid k}(i)=\frac{\lambda_{k}(i) \sum_{j=1}^{d} \Gamma_{j i} \mu_{k-1 \mid k-1}(j)}{\sum_{l=1}^{d} \lambda_{k}(l) \sum_{m=1}^{d} \Gamma_{m l} \mu_{k-1 \mid k-1}(m)} \end{aligned}$$

IMM迭代计算方程

1. for 对于每一个模型 i do
   模型预测概率 $$\mu_{k \mid k-1}(i)=p\left(r_{k}=i \mid y^{k-1}\right)=\sum_{j=1}^{d} \Gamma_{ji} \mu_{k-1 \mid k-1}(j)$$ 混合模型概率 $$\begin{aligned} \mu_{k \mid k-1}^{j \mid i}=p\left(r_{k-1}=j \mid r_{k}=i, y^{k-1}\right)=\frac{\Gamma_{ji} \mu_{k-1 \mid k-1}(j)}{\sum_{m=1}^{d} \Gamma_{m i} \mu_{k-1 \mid k-1}(m)} \end{aligned}$$ 混合状态和协方差 $$\hat{\boldsymbol{x}}_{k-1 \mid k-1}^{0 i}=\sum_{j=1}^{d}\mu_{k \mid k-1}^{j \mid i}\hat{\boldsymbol{x}}_{k-1 \mid k-1}^{j}$$ $$\boldsymbol{P}_{k-1 \mid k-1}^{0 i}=\sum_{j=1}^{d} \boldsymbol{\mu}_{k \mid k-1}^{j \mid i}\left\{\boldsymbol{P}_{k-1 \mid k-1}^{j}+\left[\hat{\boldsymbol{x}}_{k-1 \mid k-1}^{j}-\boldsymbol{x}_{k-1 \mid k-1}^{0 i}\right]\left[\hat{\boldsymbol{x}}_{k-1 \mid k-1}^{j}-\hat{\boldsymbol{x}}_{k-1 \mid k-1}^{0 i}\right]^{\mathrm{T}}\right\}$$ end for
2. for 对于每一个模型 i do
   预测目标状态 $$\hat{\boldsymbol{x}}_{k \mid k-1}^{i}=\boldsymbol{F}_{i} \hat{\boldsymbol{x}}_{k-1 \mid k-1}^{0 i}+\boldsymbol{u}_{i}$$ 预测协方差 $$\boldsymbol{P}_{k \mid k-1}^{i}=\boldsymbol{F}_{i} \boldsymbol{P}_{k-1 \mid k-1}^{0 i} \boldsymbol{F}_{i}^{T}+\boldsymbol{Q}_{i}$$ 状态更新 $$\hat{\boldsymbol{x}}_{k \mid k}^{i}=\hat{\boldsymbol{x}}_{k \mid k-1}^{i}+\boldsymbol{P}_{k \mid k-1}^{i} \boldsymbol{H}^{T}\left(\boldsymbol{H} \boldsymbol{P}_{k \mid k-1}^{i} \boldsymbol{H}^{T}+\boldsymbol{R}_{k}\right)^{-1}\left(\boldsymbol{y}_{k}-\boldsymbol{H} \hat{\boldsymbol{x}}_{k \mid k-1}^{i}\right)$$ 协方差更新 $$\boldsymbol{P}_{k \mid k}^{i}=\boldsymbol{P}_{k \mid k-1}^{i}-\boldsymbol{P}_{k \mid k-1}^{i} \boldsymbol{H}^{\mathrm{T}}\left(\boldsymbol{H} \boldsymbol{P}_{k \mid k-1}^{i} \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{R}_{k}\right)^{-1} \boldsymbol{H} \boldsymbol{P}_{k \mid k-1}^{i}$$ 模型似然函数 $$\lambda_{k}(i)=N\left(\boldsymbol{y}_{k} ; \boldsymbol{H} \hat{\boldsymbol{x}}_{k \mid k-1}^{i}, \boldsymbol{H} \boldsymbol{P}_{k \mid k-1}^{i} \boldsymbol{H}^{T}+\boldsymbol{R}_{k}\right)$$ end for
   模型概率： $$\begin{aligned} \mu_{k \mid k}(i)=\frac{\lambda_{k}(i) \sum_{j=1}^{d} \Gamma_{j i} \mu_{k-1 \mid k-1}(j)}{\sum_{l=1}^{d} \lambda_{k}(l) \sum_{m=1}^{d} \Gamma_{m l} \mu_{k-1 \mid k-1}(m)} \end{aligned}$$ 条件均值： $$\hat{\boldsymbol{x}}_{k \mid k}=\sum_{i=1}^{d} \hat{\boldsymbol{x}}_{k \mid k}^{i} \boldsymbol{\mu}_{k \mid k}(i)$$ 条件协方差： $$\boldsymbol{P}_{k \mid k}=\sum_{i=1}^{d}\left[\boldsymbol{P}_{k \mid k}^{i}+\left(\hat{\boldsymbol{x}}_{k \mid k}-\hat{\boldsymbol{x}}_{k \mid k}^{i}\right)\left(\hat{\boldsymbol{x}}_{k \mid k}-\hat{\boldsymbol{x}}_{k \mid k}^{i}\right)^{\mathrm{T}}\right] \boldsymbol{\mu}_{k \mid k}(i)$$

仿真

clc;close all;clear all;

simTime=100;      %仿真迭代次数
T=1;

d = 3;%模型数

w2=3*2*pi/360;     %模型2转弯率3度
w3=-3*2*pi/360;    %模型3转弯率-3度
H=[1,0,0,0;0,0,1,0];                      %模型量测矩阵
G=[T^2/2,0;T,0;0,T^2/2;0,T];              %模型过程噪声加权矩阵
r=100;                                 %20 2000
R=[r,0;0,r];                           %模型量测噪声协方差矩阵
Q=G*[10,0;0,10]*G';                      %模型过程噪声协方差矩阵

F(:,:,1)=[1,T,0,0;0,1,0,0;0,0,1,T;0,0,0,1];     %模型1状态转移矩阵

F(:,:,2)=[1,sin(w2*T)/w2,0,(cos(w2*T)-1)/w2;
    0,cos(w2*T),0,sin(w2*T);
    0,(1-cos(w2*T))/w2,1,sin(w2*T)/w2;
    0,-sin(w2*T),0,cos(w2*T)];            %模型2状态转移矩阵 左转弯

F(:,:,3)=[1,sin(w3*T)/w3,0,(cos(w3*T)-1)/w3;
    0,cos(w3*T),0,sin(w3*T);
    0,(1-cos(w3*T))/w3,1,sin(w3*T)/w3;
    0,-sin(w3*T),0,cos(w3*T)];            %模型3状态转移矩阵 右转弯

x = zeros(4,simTime);
z_k = zeros(2,simTime);         %含噪声量测数据
measureNoise = zeros(2,simTime);
measureNoise = sqrt(R)*randn(2,simTime);  %产生量测噪声
x(:,1)=[1000,200,1000,200]';
z_k(:,1)=H*x(:,1)+measureNoise(:,1);
for a=2:simTime
    if (a>=20)&&(a<=40) 
        x(:,a)=F(:,:,2)*x(:,a-1);      %20--40s左转 
    elseif (a>=60)&&(a<=80) 
       x(:,a)=F(:,:,3)*x(:,a-1);        %60--80s右转 
    else
        x(:,a)=F(:,:,1)*x(:,a-1);      %匀速直线运动
    end
z_k(:,a)=H*x(:,a)+measureNoise(:,a);
end

xkki(:,1) = x(:,1);      %模型1IMM算法状态估计值
xkki(:,2) = x(:,1);      %模型2IMM算法状态估计值
xkki(:,3) = x(:,1);      %模型3IMM算法状态估计值

xkk = zeros(4,simTime);      %IMM算法模型综合状态估计值
pkk=zeros(4,4,simTime);      %IMM算法模型综合状态协方差矩阵
pkki(:,:,1)=zeros(4,4);
pkki(:,:,2)=zeros(4,4);
pkki(:,:,3)=zeros(4,4);      %IMM算法各模型协方差矩阵

xkk(:,1)=x(:,1);

Sigmaji=[0.9,0.05,0.05;
         0.1,0.8,0.1;
         0.05,0.15,0.8];    %模型转移概率矩阵

ukk=zeros(3,simTime);
ukk(:,1)=[0.3 0.3 0.4]';  %IMM算法模型概率

for t=1:simTime-1
    
    %第一步Interacting（只针对IMM算法）
    ukk_1=Sigmaji'*ukk(:,t);
    
    for i = 1:d
        uji(:,i)=(1/ukk_1(i))*Sigmaji(:,i).*ukk(:,t);%计算模型混合概率     
    end

    % 计算各模型滤波初始化条件
    % 各模型滤波初始状态
    for i = 1:d
        x0(:,i) = xkki * uji(:,i);
    end 
    
    %各模型滤波初始状态协方差矩阵
    for i = 1:d
        temp = zeros(4,4);
        for k = 1:d
            temp = temp + pkki(:,:,k)+(xkki(:,i)-x0(:,i))*(xkki(:,i)-x0(:,i))'*uji(k,i);
        end
        P0(:,:,i) = temp;  
    end
    
    % kalman滤波并且计算似然函数值
    for i = 1:d
        [xkki(:,i),pkki(:,:,i),xkk_1,pkk_1] = Kalman(z_k(:,t),x0(:,i),F(:,:,i),H,P0(:,:,i),Q,R);
        lambda(i) = (1/sqrt(abs(2*pi*(det(H*pkk_1*H'+R)))))*exp((-1/2)*((z_k(:,t)-H*xkk_1)'*inv(H*pkk_1*H'+R)*(z_k(:,t)-H*xkk_1)));
    end
    lambda = lambda/sum(lambda);
%     条件模型概率
    for i = 1:d
        ukk(i,t+1) = lambda(i) * ukk_1(i)./lambda*ukk_1;
    end
    ukk(:,t+1) = ukk(:,t+1)/sum(ukk(:,t+1));
%     ukk(:,t+1) = 1/(lambda*ukk_1).*lambda'.*ukk_1;
    xkk(:,t+1) = xkki * ukk(:,t+1);
end

figure
hold on
grid on
plot(x(1,:),x(3,:));
plot(xkk(1,:),xkk(3,:));
plot(z_k(1,:),z_k(2,:));
xlabel('x axis(m)');
ylabel('y axis(m)');
legend('真实值','预测值','测量值');

figure
hold on
grid on
plot(ukk(1,:),'k:','linewidth',2);
plot(ukk(2,:),'r-.','linewidth',2);
plot(ukk(3,:),'b--','linewidth',2);
title('IMM模型概率曲线');
xlabel('次数序号(s)'); ylabel('模型概率');
legend('模型1','模型2','模型3');

function [x_est,P_k_k,x_pre,P] = Kalman(z_k,x_est_k_minus1,F,H,P_k,Q,R)
   x_pre = F*x_est_k_minus1;
   P = F*P_k*F' + Q;
   
   z_pre = H*x_pre;
   S = H*P*H' + R;
   K = P*H'/(S);
   
   x_est = x_pre + K*(z_k - z_pre);
   P_k_k = (eye(size(K*H,1))-K*H)*P;
end