UKF

不敏卡尔曼滤波

首先讨论这样的一个问题一个满足高斯分布的随机变量经过非线性系统的输出随机变量的分布如何确定呢？
如果采用蒙特卡洛估方法。下图，在原高斯分布中采样，很多采样点（该图中是500000个画出来的），将采样点通过非线性变换，再统计变换后的结果的均值与方差，近似用一个高斯分布表示。这种方法的缺点很明显，计算量巨大，特别是在高维时。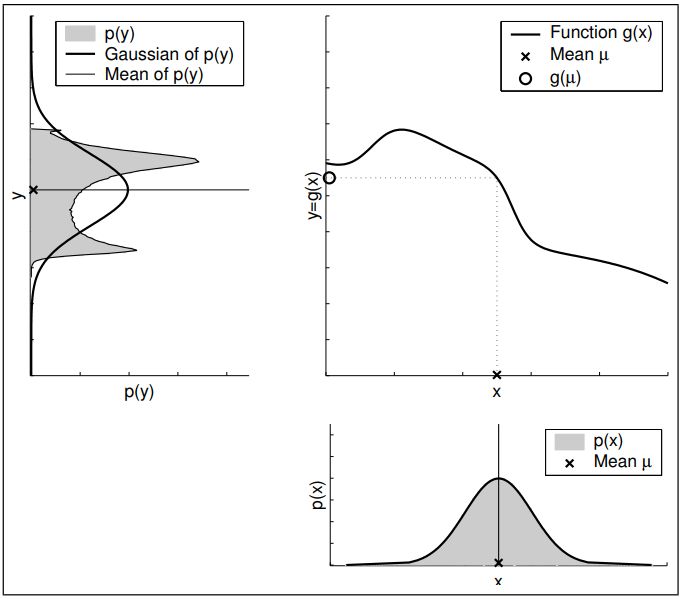

或者说我们如何得到输出变量的一阶二阶标准矩？
考虑一个随机变量 $\boldsymbol{x} \in \mathbb{R}^{n}$ 和非线性变换 $\boldsymbol{g}: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$。$z$的均值可以表示为

$$E(z)=\int g(\boldsymbol{x}) p(\boldsymbol{x}) d \boldsymbol{x}$$

实际上这样的计算在大多数情况下是无法计算的（工程）。
而在目标跟踪的过程中其实只要能够数值近似$E(z)$和$D(z)$,在这里采用不敏变换

不敏变换（UT）

基本思路：通过定义域上非均匀采样点的函数值进行加权求和

UT变换的步骤：

1. Choose Sigma Points
2. Transform Sigma Points
3. Compute Weighted Mean And Covariance of Transformed Sigma Points

Choose Sigma Points

$N$维的高斯分布选择$2N+1$个Sigma点$\chi^{1},\chi^{2}\cdots \chi^{2N+1}$，$w^{1}，w^{2}\cdots w^{2N+1}$表示对应的权值，要求Sigma点的均值方差收敛于原均值与方差

$$\begin{array}{l} \frac{1}{2N+1} \sum_{i=1}^{2N+1} w^{i} \chi^{i}=E(\boldsymbol{x}) \\ \frac{1}{2N+1} \sum_{i=1}^{2N+1} w^{i}\left[\chi^{i}-E(\boldsymbol{x})\right]\left[\chi^{i}-E(\boldsymbol{x})\right]^{\mathrm{T}}=\operatorname{cov}(\boldsymbol{x}) \end{array}$$

令 ${Z}^{i}=\boldsymbol{g}\left(\chi^{i}\right), i=1, \cdots, 2N+1$ 表示在第 $i$ 个 $\operatorname{sigma}$ 点处的函数值。 $z$ 均值的 UT $\mathbb{近}$
似可以表示为

$$\widehat{E(z)}=\frac{1}{2N+1} \sum_{i=1}^{2N+1} w^{i} {Z}^{i}$$

z的协方差矩阵以及 z 和 x 的互协方差，通过 UT 近似计算可以得到

$$\begin{aligned} \widehat{\operatorname{cov}(z)} &=\frac{1}{2N+1} \sum_{i=1}^{2N+1} w^{i}\left[Z^{i}-\widehat{E(z)}\right]\left[{Z}^{i}-\widehat{E(z)}\right]^{\mathrm{T}} \\ \widehat{\operatorname{cov}(x, z)} &=\frac{1}{2N+1} \sum_{i=1}^{2N+1} w^{i}\left[\chi^{i}-E(x)\right]\left[{Z}^{i}-\widehat{E(z)}\right]^{\mathrm{T}} \end{aligned}$$

Sigma点的选择有很多种在这里选择，采用如下的方法：

$$\chi^{i} = \boldsymbol{\mu} + \boldsymbol{\sigma}^{i}$$

其中

• $\boldsymbol{\mu}=E(\boldsymbol{x})$
• $\boldsymbol{\sigma}^{1} = \boldsymbol{0}$，$[\boldsymbol{\sigma}^{2} \cdots \boldsymbol{\sigma}^{N+1}] = \boldsymbol{A}(\boldsymbol{\sigma}^{N+i+1}=-\boldsymbol{\sigma}^{i+1}, i=1, \cdots, N)$,$\boldsymbol{A}$是$(N+\kappa)\boldsymbol{\Sigma}$的Cholesky分解，即满足$\boldsymbol{A}\boldsymbol{A}^T=(N+\kappa)\boldsymbol{\Sigma}$

$\chi^{i}$对应的权值为

$$w^{i}=\left\{\begin{array}{ll} \kappa /(N+\kappa) & i=1 \\ 0.5 /(N+\kappa) & i=2, \cdots, 2 N+1 \end{array}\right.$$

用图像可以形象的表示出来(2维的情况)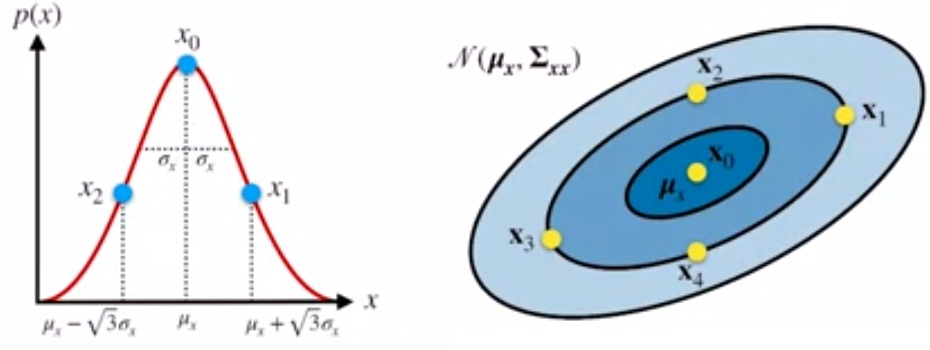

不敏卡尔曼滤波算法

(1) 确定 sigma 点 $\chi_{k-1}^{1}, \cdots, \chi_{k-1}^{2N+1}$ 和权值 $w^{1}, \cdots, w^{2N+1}$
(2) 计算 sigma 点的转换 $\chi_{k}^{i}=f\left(\chi_{k-1}^{i}\right), i=1, \cdots, 2N+1$。
(3) 计算状态预测统计量

$$\begin{array}{c} \hat{\boldsymbol{x}}_{k \mid k-1}=\sum_{i=1}^{2N+1} w^{i} \chi_{k}^{i} \\ \boldsymbol{P}_{k \mid k-1}=\boldsymbol{Q}_{k}+\sum_{i=1}^{2N+1} w^{i}\left(\chi_{k}^{i}-\hat{\boldsymbol{x}}_{k \mid k-1}\right)\left(\chi_{k}^{i}-\hat{\boldsymbol{x}}_{k \mid k-1}\right)^{\mathrm{T}} \end{array}$$

(4) 确定均值 $\hat{\boldsymbol{x}}_{k \mid k-1}$ 和方差 $\boldsymbol{P}_{k \mid k-1}$ 的 $\operatorname{sigma}$ 点 $\chi_{k}^{1}, \cdots, \chi_{k}^{2N+1}$ 和权值 $w^{1}, \cdots, w^{2N+1}$
(5) 计算 sigma 点的转换 $\nu_{k}^{i}=\boldsymbol{h}\left(\chi_{k}^{i}\right), i=1, \cdots, 2N+1$。
(6)计算观测预测统计量

$$\begin{array}{l} \hat{\boldsymbol{y}}_{k \mid k-1}=\sum_{i=1}^{2N+1} w^{i} \boldsymbol{\nu}_{k}^{i} \\ \boldsymbol{S}_{k}=\boldsymbol{R}_{k}+\sum_{i=1}^{2N+1} w^{i}\left(\nu_{k}^{i}-\hat{\boldsymbol{y}}_{k \mid k-1}\right)\left(\nu_{k}^{i}-\hat{\boldsymbol{y}}_{k \mid k-1}\right)^{\mathrm{T}} \\ \boldsymbol{\Psi}_{k}=\sum_{i=1}^{2N+1} w^{i}\left(\chi_{k}^{i}-\hat{\boldsymbol{x}}_{k \mid k-1}\right)\left(\nu_{k}^{i}-\hat{\boldsymbol{y}}_{k \mid k-1}\right)^{\mathrm{T}} \end{array}$$

(7) 计算后验均值和方差矩阵

$$\begin{aligned} \hat{\boldsymbol{x}}_{k} &=\hat{\boldsymbol{x}}_{k \mid k-1}+\boldsymbol{\Psi}_{k} \boldsymbol{S}_{k}^{-1}\left(\boldsymbol{y}_{k}-\hat{\boldsymbol{y}}_{k \mid k-1}\right) \\ \boldsymbol{P}_{k \mid k}&= \boldsymbol{P}_{k \mid k-1}-\boldsymbol{\Psi}_{k} \boldsymbol{S}_{k}^{-1} \boldsymbol{\Psi}_{k}^{\mathrm{T}} \end{aligned}$$