卡尔曼滤波

假设条件

A1 目标动态和观测方程是线性的：

$\begin{array}{l} \mathbf{x}_{k}= \mathbf{F} \mathbf{x}_{k-1}+\mathbf{v}_{k} \\ \mathbf{y}_{k}=\mathbf{H} x_{k}+\mathbf{w}_{k} \end{array}$

A2 $\mathbf{v}_{k}$ 和 $\mathbf{w}_{k}$ 是均值为突且噪声协方差分别为 $\mathbf{Q}_{k}$ 和 $\mathbf{R}_{k}$ 的高斯白噪声
A3 $k-1$ 时刻后验概率密度 $p\left(\mathbf{x}_{k-1} \mid \mathbf{y}^{k-1}\right)$ 是均值为 $\hat{\mathbf{x}}_{k-1| k-1}$，方差为$\mathbf{P}_{k-1 | k-1}$的高斯形式。

高斯分布与高斯乘积定理

首先规定一下高斯密度函数，由于求解后验概率密度时需要有概率密度函数相乘，所以我们很感兴趣两个概率密度函数相乘后满足怎样的分布

$N(z ; \mathbf{\mu}, \mathbf{\Sigma})=\frac{1}{\sqrt{2 \pi|\mathbf{\Sigma}| }} \exp \left[-(z-\mathbf{\mu})^{\mathrm{T}} \mathbf{\Sigma}^{-1}(z-\mathbf{\mu}) / 2\right]$

高斯乘积定理: 给定 $\mathbf{x}_{1}, \mathbf{\mu}_{1} \in \mathbb{R}^{d_{1}}, \mathbf{H} \in \mathbb{R}^{d_{2} \times d_{1}}, \mathbf{x}_{2} \in \mathbb{R}^{d_{2}}$ 和正定矩阵$\mathbf{P}_{1}, \mathbf{P}_{2}$

$N\left(\mathbf{x}_{2} ; \mathbf{H} \mathbf{x}_{1}, \mathbf{P}_{2}\right) N\left(\mathbf{x}_{1} ; \mathbf{\mu}_{1}, \mathbf{P}_{1}\right)=N\left(\mathbf{x}_{2} ; \mathbf{H} \mathbf{\mu}_{1}, \mathbf{P}_{3}\right) N\left(\mathbf{x}_{1} ; \mathbf{\mu}, \mathbf{P}\right)$

其中

$\begin{array}{c} \mathbf{P}_{3}=\mathbf{H} \mathbf{P}_{1} \mathbf{H}^{\mathrm{T}}+\mathbf{P}_{2} \\ \mathbf{\mu}=\mathbf{\mu}_{1}+\mathbf{K}\left(\mathbf{x}_{2}-\mathbf{H} \mathbf{\mu}_{1}\right) \\ \mathbf{P}=\mathbf{P}_{1}+\mathbf{K} \mathbf{H} \mathbf{P}_{1} \\ \mathbf{K}=\mathbf{P}_{1} \mathbf{H}^{\mathrm{T}} \mathbf{P}_{3}^{-1} \end{array}$

卡尔曼迭代

预测函数

状态转移函数

$p\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{k-1}\right)=N\left(\boldsymbol{x}_{k} ; \boldsymbol{F} \boldsymbol{x}_{k-1}, \boldsymbol{Q}_{k}\right)$

假定$k-1$时刻的目标状态后验概率密度函数$p(\boldsymbol{x}_{k-1} | \boldsymbol{y}^{k-1}) = N(\boldsymbol{x}_{k-1};\left.\hat{\boldsymbol{x}}_{k-1 \mid k-1}, \boldsymbol{P}_{k-1 \mid k-1}\right)$

预测概率密度函数

$\begin{aligned} p\left(\boldsymbol{x}_{k} \mid \boldsymbol{y}^{k-1}\right) &=\int p\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{k-1}\right) p\left(\boldsymbol{x}_{k-1} \mid \boldsymbol{y}^{k-1}\right) \mathrm{d} \boldsymbol{x}_{k-1} \\ &=\int N\left(\boldsymbol{x}_{k} ; \boldsymbol{F} \boldsymbol{x}_{k-1}, \boldsymbol{Q}_{k}\right) N\left(\boldsymbol{x}_{k} ; \hat{\boldsymbol{x}}_{k-1 \mid k-1}, \boldsymbol{P}_{k \mid k-1}\right) \mathrm{d} \boldsymbol{x}_{k-1} \end{aligned}$

应用高斯乘积定理，可以得到预测概率密度的表达式为

$\begin{aligned} p\left(\boldsymbol{x}_{k} \mid \boldsymbol{y}^{k-1}\right)=& \int N\left(\boldsymbol{x}_{k} ; \hat{\boldsymbol{x}}_{k \mid k-1}, \boldsymbol{P}_{k \mid k-1}\right) \times \\ & N\left(\boldsymbol{x}_{k-1} ; \hat{\boldsymbol{x}}_{k-1 \mid k-1}+G_{k}\left(\boldsymbol{x}_{k}-\hat{\boldsymbol{x}}_{k \mid k-1}\right), \boldsymbol{M}_{k}\right) \mathrm{d} \boldsymbol{x}_{k-1} \\ =& N\left(\boldsymbol{x}_{k} ; \hat{\boldsymbol{x}}_{k \mid k-1}, \boldsymbol{P}_{k \mid k-1}\right) \end{aligned}$

这一操作即为标准卡尔曼滤波预测，其伪函数形式可写为

$\left[\hat{\boldsymbol{x}}_{k \mid k-1}, \boldsymbol{P}_{k \mid k-1}\right]=K F_{p}\left[\hat{\boldsymbol{x}}_{k-1 \mid k-1}, \boldsymbol{P}_{k-1 \mid k-1}, \boldsymbol{F}, \boldsymbol{Q}\right]$

其中

$\begin{array}{c} \hat{\boldsymbol{x}}_{k \mid k-1}=\boldsymbol{F} \hat{\boldsymbol{x}}_{k-1 \mid k-1} \\ \boldsymbol{P}_{k \mid k-1}=\boldsymbol{F} \boldsymbol{P}_{k-1 \mid k-1} \boldsymbol{F}^{\mathrm{T}}+\boldsymbol{Q} \end{array}$

似然函数与归一化因子

似然函数：$p( \boldsymbol{y}_{k}\mid \boldsymbol{x}_{k}) = N(\boldsymbol{y}_{k};\boldsymbol{Hx}_k,\boldsymbol{R}_k)$

归一化因子：

$\begin{array}{c} p\left(\boldsymbol{y}^{k} \mid \boldsymbol{y}^{k-1}\right) =\int p\left(\boldsymbol{y}_{k} \mid \boldsymbol{x}_{k}\right) p\left(\boldsymbol{x}_{k} \mid \boldsymbol{y}^{k-1}\right) \mathrm{d} \boldsymbol{x}_{k} \\ =\int N\left(\boldsymbol{y}_{k} ; \boldsymbol{H} \boldsymbol{x}_{k}, \boldsymbol{R}_{k}\right) N\left(\boldsymbol{x}_{k} ; \hat{\boldsymbol{x}}_{k / k-1}, \boldsymbol{P}_{k \mid k-1}\right) \mathrm{d} \boldsymbol{x}_{k} \\ =N\left(\boldsymbol{y}_{k} ; \boldsymbol{y}_{k \mid k-1}, \boldsymbol{S}_{k}\right) \end{array}$

其中$\hat{\boldsymbol{y}}_{k \mid k-1}=\boldsymbol{H} \hat{\boldsymbol{x}}_{k \mid k-1}, \boldsymbol{S}_{k}=\boldsymbol{H} \boldsymbol{P}_{k \mid k-1} \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{R}_{k}$

后验概率密度函数

$p\left(\boldsymbol{x}_{k} \mid \boldsymbol{y}^{k}\right)=\frac{N\left(\boldsymbol{y}_{k} ; \boldsymbol{H} \boldsymbol{x}_{k}, \boldsymbol{R}_{k}\right) N\left(\boldsymbol{x}_{k} ; \hat{\boldsymbol{x}}_{k \mid k-1}, \boldsymbol{P}_{k \mid k-1}\right)}{N\left(\boldsymbol{y}_{k} ; \boldsymbol{y}_{k \mid k-1}, \boldsymbol{S}_{k}\right)}$

再次利用高斯乘积定理，后验概率密度可以表示为

$\begin{array}{c} p\left(\boldsymbol{x}_{k} \mid \boldsymbol{y}^{k}\right)=N\left(\boldsymbol{x}_{k} ; \hat{\boldsymbol{x}}_{k \mid k}, \boldsymbol{P}_{k \mid k}\right) \end{array}$

其中

$\hat{\boldsymbol{x}}_{k \mid k}=\hat{\boldsymbol{x}}_{k \mid k-1}+\boldsymbol{P}_{k \mid k-1} \boldsymbol{H}^{\mathrm{T}} \boldsymbol{S}_{k}^{-1}\left(\boldsymbol{y}_{k}-\hat{\boldsymbol{y}}_{k \mid k-1}\right) \\ \boldsymbol{P}_{k \mid k}=\boldsymbol{P}_{k \mid k-1}-\boldsymbol{P}_{k \mid k-1} \boldsymbol{H}^{\mathrm{T}} \boldsymbol{S}_{k}^{-1} \boldsymbol{H} \boldsymbol{P}_{k \mid k-1}$

到这里其实卡尔曼滤波的迭代估计就结束了，接下来给出一个算法的流程

算法流程

卡尔曼滤波方程：

计算预测均值和方差矩阵
$\begin{array}{c} \hat{\boldsymbol{x}}_{k \mid k-1}=\boldsymbol{F} \hat{\boldsymbol{x}}_{k-1 \mid k-1} \\ \boldsymbol{P}_{k \mid k-1}=\boldsymbol{F} \boldsymbol{P}_{k-1 \mid k-1} \boldsymbol{F}^{\mathrm{T}}+\boldsymbol{Q}_{k} \end{array}$
计算观测预测、新息方差矩阵和卡尔曼滤波增益
$\begin{array}{c} \hat{\boldsymbol{y}}_{k \mid k-1}=\boldsymbol{H} \hat{\boldsymbol{x}}_{k \mid k-1}\\ \boldsymbol{S}_{k}=\boldsymbol{H} \boldsymbol{P}_{k \mid k-1} \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{R} \\ \boldsymbol{K}_{k}=\boldsymbol{P}_{k \mid k-1} \boldsymbol{H}^{\mathrm{T}} \boldsymbol{S}_{k}^{-1} \end{array}$
计算后验均值和方差矩阵
$\begin{array}{c} \hat{\boldsymbol{x}}_{k \mid k}=\hat{\boldsymbol{x}}_{k \mid k-1}+\boldsymbol{K}_{k}\left(\boldsymbol{y}_{k}-\hat{\boldsymbol{y}}_{k \mid k-1}\right)\\ \boldsymbol{P}_{k \mid k}=\left(\boldsymbol{I}-\boldsymbol{K}_{k} \boldsymbol{H}\right) \boldsymbol{P}_{k \mid k-1} \end{array}$

matlab仿真

根据算法流程可以写出KalmanFilter的一步迭代函数

function [x_est,P_k_k] = KalmanFilter(z_k,x_est_k_minus1,F,H,P_k,Q,R)
   x_pre = F*x_est_k_minus1;
   P = F*P_k*F' + Q;
   
   z_pre = H*x_pre;
   S = H*P*H' + R;
   K = P*H'/(S);
   
   x_est = x_pre + K*(z_k - z_pre);
   P_k_k = (eye(size(K*H,1))-K*H)*P;
end

参数的解释
输入参数:

$z_k$ $k$时刻的量测值
$x_est_k_minus1$ $k-1$时刻的状态后验估计
$F$ 系统状态转移矩阵
$H$ 量测矩阵
$P_k$ $k-1$时刻的状态后验估计协方差矩阵
$Q$ 过程噪声协方差矩阵
$R$ 测量噪声协方差矩阵
输出参数:
$x_est$ $k$时刻状态后验估计
$P_k_k$ $k$时刻状态后验估计协方差矩阵

下面给出一个实际代码的示例

clc;close all;clear all

for kk = 1:100

T = 0.01;
L = 1000;

F = [1 T;
     0 1];
x(:,1) = [0;1];
y(1) = randn;

H = [1 0];

v = randn(1,L);
w = 1*randn(1,L);

for i =2:L
    x(:,i) = F*x(:,i-1)+[T^2/2;T]*v(i);
    y(i) = H*x(:,i)+w(i); 
end

Q =[1/3*T^3 1/2*T^2; 1/2*T^2 T]*var(v);
R = 2*var(w);

xe = zeros(2,L);
xe(:,1) = randn(2,1);
P = eye(2);

xe = zeros(2,L);

for i=2:L
    [xe(:,i),P] = KalmanFilter(y(i),xe(:,i-1),F,H,P,Q,R);
end

Err_e(kk,:) = xe(1,:)-x(1,:);
Err_m(kk,:) = w;

end

%% 对最后一次结果进行展示
figure
hold on
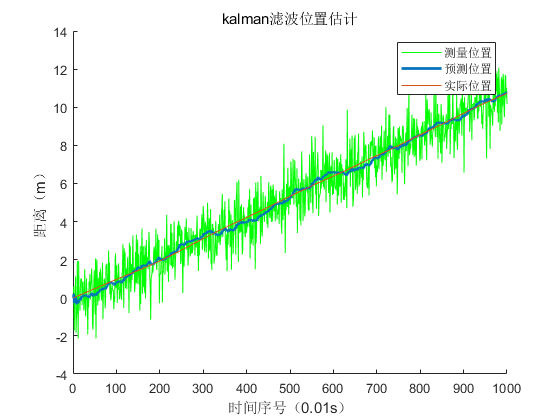
plot(y(1,:),'g');
plot(xe(1,:),'linewidth',2);
plot(x(1,:));
legend('测量位置','预测位置','实际位置');
xlabel('时间序号（0.01s）');
ylabel('距离（m）');
title('kalman滤波位置估计')

figure
hold on
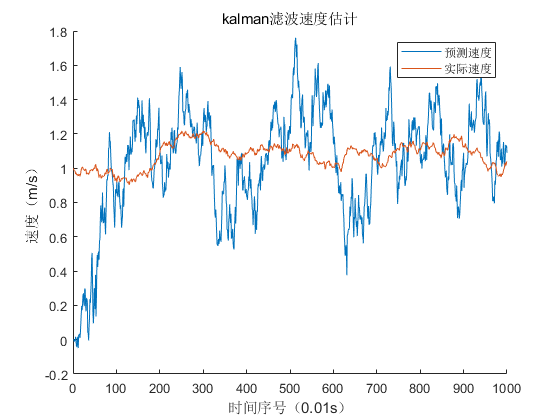
plot(xe(2,:));
plot(x(2,:));
legend('预测速度','实际速度');
xlabel('时间序号（0.01s）');
ylabel('速度（m/s）');
title('kalman滤波速度估计')
%% 计算状态估计误差

Var_E = var(mean(Err_e));
Var_M = var(mean(Err_m));

figure
hold on
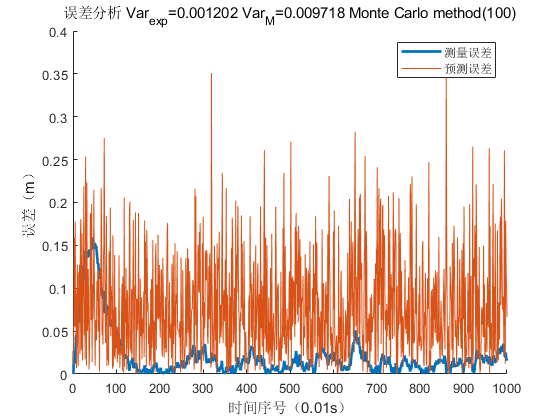
plot(abs(mean(Err_e)),'linewidth',2);
plot(abs(mean(Err_m)));
legend('测量误差','预测误差');
xlabel('时间序号（0.01s）');
ylabel('误差（m）');
title(['误差分析 Var_{exp}=' num2str(Var_E) ' Var_{M}=' num2str(Var_M) ' Monte Carlo method(100)'] );

运行可以得到

Bulijiojio Blog

KF