Bulijiojio Blog

日常摸鱼划水的虾皮--如果公式不能正常显示请使用Chrome浏览器并安装Tex All the Things插件

0%

PDradar

发表于 更新于 分类于

雷达信号处理基基础

脉冲体制

回波信号分析

以线性调频（LFM）为例，在一次发射周期中，发射信号相位为

发射时刻与接收到回波的时刻间时延为（v为径向速度且为匀速）

接收信号相位为

那么经过前级的处理可以得到中频信号的相位为

假设再一次相参处理过程中脉冲积累数为M，那么第n次脉冲周期中（T）$1 \leq n \leq M$

其中 $R_n = R_{0} - v(n-1)T$ , $\tau_n = \frac{2R_n}{c} = \tau_n(0)$,$DR$ 为占空比。

注：

  • $P_{IF}=P_R-P_L$,其中本振信号相位$P_D=2\pi(t-\frac{2R}c+\phi_D)(f_R-f_I+\frac B 2)$，$\phi_D$最终归入$\phi_{IF}$这个系数中，后级处理暂不考虑。

  • $R_n$指第n个脉冲发射时刻，目标与雷达之间的距离，因此$R_n=R_0-v(n-1)$

  • $\tau_n$由如下得到：
    $\tau_n=\frac {2(R_n-v\frac {\tau_n} 2)}{c} \Rightarrow\tau_n=\frac{2R_n}{c+v}$
    解得 $\tau_n=\frac{2R_n}{c+v}$
    因此，$\tau_n=\frac{2R_n}{c+v}\approx\frac{2R_n}{c}=\frac{2(R_0-v(n-1)T)}{c}$,当$R_0 \gg v(n-1)T $时，$\tau_n \approx \tau_0$。

匹配滤波原理简述

匹配滤波器（match filter）是最佳线性滤波器的一种，该滤波器的准则是输出信噪比最大，常用于通信、雷达等系统的接收机中，下面对其冲激响应/系统函数进行推导。

设该滤波器传递函数为$H(f)$，冲激响应为$h(t)$，输入信号为

其中$s(t)$为输入信号，$n(t)$为高斯白噪声。

设输入信号的频谱密度函数为$S(f)$，而高斯白噪声的单边功率谱为$\frac{n_0}2$，其中$n_0$为高斯白噪声单边功率谱密度。

那么经过系统响应函数为$H(j\omega)$的LTI系统后，设$s_0(t)$为信号的输出，其大小为

而又已知输出高斯白噪声的功率谱密度等于输入白噪声的功率谱密度乘以系统传递函数模值的平方，即输出噪声功率为：

因此，在采样时刻$t_0$上，输出信号瞬时功率和噪声平均功率之比为：

利用柯西-施瓦兹不等式

该等式当且仅当$f_1(x) = kf^{*}_{2}(x)$时取最大值,其中$k$为任意常数。那么令$f_1(x) = H(f),f_2(x)=H(f)e^{j2\pi ft_0}$可以得到：

其中E为信号的能量。而且当且仅当$H(f) = k S^*(f)e^{-j2\pi ft_0}$时，$r_0$取得最大值。

对$H(f)$求逆FFT变换，可得滤波器的冲激响应

由上式可知匹配滤波器的冲激响应就是信$s(t)$的镜像，只不过存在一个$t_0$的时延。
也可以将匹配滤波的过程理解为一个求相关的过程，当$t_0$时刻信号进入滤波器时，与滤波器系数进行卷积，相当于求自相关，很明显要远大于白噪声和滤波器系数的互相关，此时信噪比可达到最大。

仿真

参数设计

首先进行参数设计

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
c = 3e8;         %光速
RF = 35e9;       %射频频率
lambda = c/RF;   %射频波长
f0 = 85e6;       %中频  85MHz
fs = 80e6;       %采样率  80MHz
T = 50e-6;       %脉冲重复周期  500u

DutyRatio = 0.1;           %占空比
Tp = DutyRatio * T;        %脉冲持续时间  5us
tp = 0:1/fs:Tp-1/fs;
NTp = length(tp);          %脉冲采样点数

B = 10e6;         %调频带宽  10MHz
k = B/Tp;         %调频斜率=带宽/脉冲持续时间

M = 32;           %发射脉冲数/脉冲积累数

t = 0:1/fs:T-1/fs;  
NT = length(t);     %一个脉冲中的采样点数，距离门数

R1 = 5000;        %目标1距离
V1 = -10;         %目标1速度
R2 = 1000;        %目标2距离
V2 =0;            %目标2速度

回波生成

如前所述

生成中频信号,同时添加噪声

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
fd1 = 2*V1/lambda; %多普勒频率1
fd2 = 2*V2/lambda; %多普勒频率1

echo1 = zeros(M,NT); %回波
tao1 = zeros(1,M); 
N_tao1 = zeros(1,M); %取整
echo2 = zeros(M,NT); %回波
tao2 = zeros(1,M);  %多普勒
N_tao2 = zeros(1,M); %取整

echo = zeros(M,NT);

t_fd = 0:(1/fs):(T*M-1/fs);

echo1_fd = exp(1i*2*pi*fd1*t_fd); %目标1在M个脉冲内引起的连续多普勒
echo2_fd = exp(1i*2*pi*fd2*t_fd); %目标2在M个脉冲内引起的连续多普勒

AD_data = zeros(M,NT);

%% 模拟生成目标回波
for m=1:1:M
    
    tao1(1,m)=2*(R1-V1*(m-1)*T)/c;
    N_tao1(1,m) = round(tao1(1,m)*fs);
    tao2(1,m)=2*(R2-V2*(m-1)*T)/c;
    N_tao2(1,m) = round(tao2(1,m)*fs);
    
    for n=1:1:NT
        if(n < N_tao1(1,m))
            echo1(m,n) = 0;
        elseif(( n>=N_tao1(1,m) ) && ( n<=(N_tao1(1,m)+NTp) ))
            echo1(m,n) = exp(1i*pi*k*((1+2*V1/c)*t(n)-tao1(1,m)).^2)*exp(-1i*2*pi*(f0-B/2)*tao1(1,m))*exp(1i*2*pi*(f0-B/2)*t(n))*echo1_fd(1,n+(m-1)*NT);
        else
            echo1(m,n) = 0;
        end
        
         if(n < N_tao2(1,m))
            echo2(m,n) = 0;
        elseif(( n>=N_tao2(1,m) ) && ( n<=(N_tao2(1,m)+NTp) ))
            echo2(m,n) = exp(1i*pi*k*((1+2*V2/c)*t(n)-tao2(1,m)).^2)*exp(-1i*2*pi*(f0-B/2)*tao2(1,m))*exp(1i*2*pi*(f0-B/2)*t(n))*echo2_fd(1,n+(m-1)*NT);
        else
            echo2(m,n) = 0;
        end
    end
    
    %------在echo中添加高斯噪声------%
    SNR1 = -5;  % 信号1的信噪比dB
    NOISE1=randn(1,NT);
    
    signal_power1 = (1/NTp)*(sum((echo1(m,:).*conj(echo1(m,:)))));
    noise_variance1 = signal_power1 / ( 10^(SNR1/10) );
    std_noise_n1 = std(NOISE1);
    NOISE1 =1/ sqrt(noise_variance1)*NOISE1;
    echo1(m,:)=echo1(m,:)+(NOISE1+1i*hilbert(NOISE1));
    
    SNR2 = 2;  % 信号2的信噪比dB
    NOISE2=randn(1,NT);

    signal_power2 = (1/NTp)*(sum((echo2(m,:).*conj(echo2(m,:)))));
    noise_variance2 = signal_power2 / ( 10^(SNR2/10) );
    std_noise_n2 = std(NOISE2);
    NOISE2 = 1/sqrt(noise_variance1)*NOISE2;
    echo2(m,:)=echo2(m,:)+(NOISE2+1i*hilbert(NOISE2));
    %------在echo中添加高斯噪声end------%
    
    echo(m,:) = echo1(m,:)+ echo2(m,:);
    AD_data(m,:) = real( echo(m,:) );
end

数字正交下变频（DDC）

正交解调框图如下

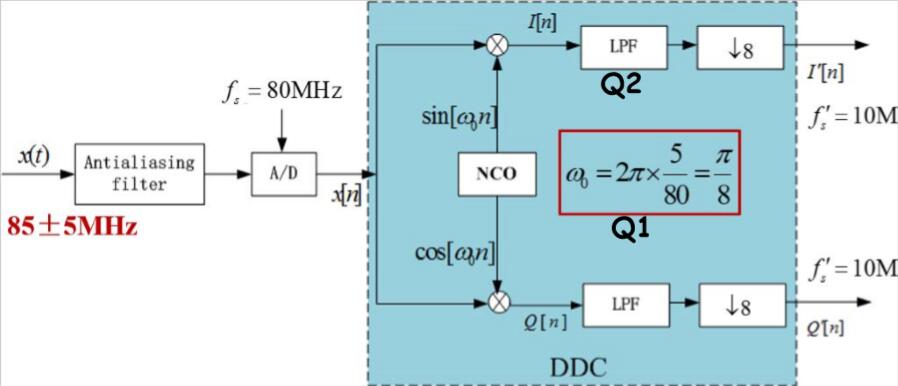
同时对下变频信号进行匹配滤波

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
%% DDC

local_I = -sin(2*pi*5e6*t);   %本振
local_Q = cos(2*pi*5e6*t);    
lowpassFilter=fir1(128,1/8); 

PC_Coff = exp(-1i*pi*k*((-Tp/2:1/10e6:Tp/2).^2));
% N_FFT = 500;   %根据运行结果调整
% H2 = conj(fft(h2,N_FFT));   %匹配滤波

for m=1:1:M  
    I_data_local(m,:) = AD_data(m,:).*local_I;
    Q_data_local(m,:) = AD_data(m,:).*local_Q;
    I_data_local_FIR(m,:)=filter(lowpassFilter,1,I_data_local(m,:));
    Q_data_local_FIR(m,:)=filter(lowpassFilter,1,Q_data_local(m,:));
    
    %-----8倍抽取------%
    Dec_I(m,:)=I_data_local_FIR(m,1:8:end);
    Dec_Q(m,:)=Q_data_local_FIR(m,1:8:end);
    
    DDC_data_out(m,:) = Dec_Q(m,:) + 1i*Dec_I(m,:);
    
    %-----匹配滤波-----%
%     temp(m,:) = fft(DDC_data_out(m,:),N_FFT);
%     PC_data_fft(m,:) = temp(m,:).*H2;  
%     PC_data_ifft(m,:) = ifft(PC_data_fft(m,:),N_FFT);
    
    PC(m,:) =conv(PC_Coff,DDC_data_out(m,:));
    PC_data(m,:) = PC(m,(length(PC_Coff)+9:end -length(PC_Coff)-9));
end

对匹配滤波的结果进行评估

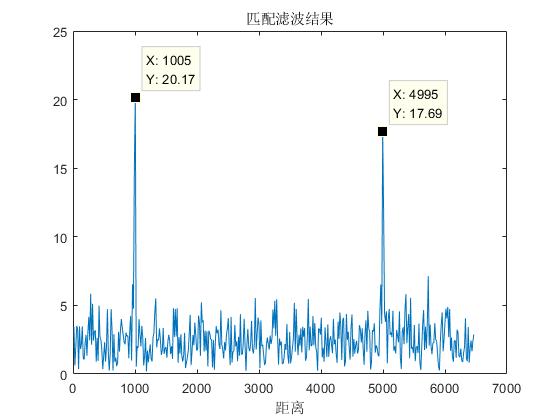
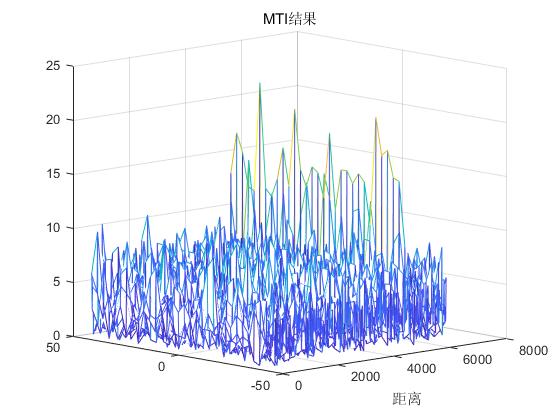
MTI与MTD

对匹配滤波后的矩阵进行一次对消

1
2
3
4
5
6
%% MTI
for m=1:1:M-1
    MTI_data(m,:) = PC_data(m+1,:) - PC_data(m,:);
end
figure
mesh(abs(MTI_data));

对MTI的矩阵进行如下处理

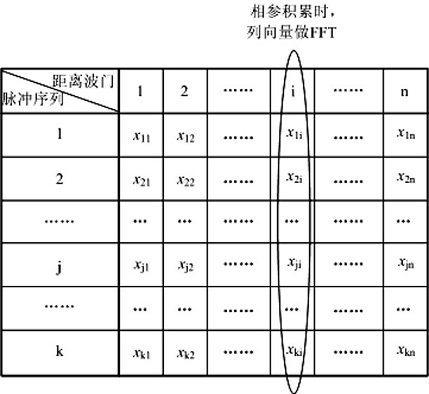
1
2
3
4
5
6
%% MTD
for l = 1:1:length(MTI_data(1,:))
    MTD_data(:,l) =fftshift( fft(MTI_data(:,l)));  %对每一列FFT（相参积累）
end
figure
mesh(abs(MTD_data));

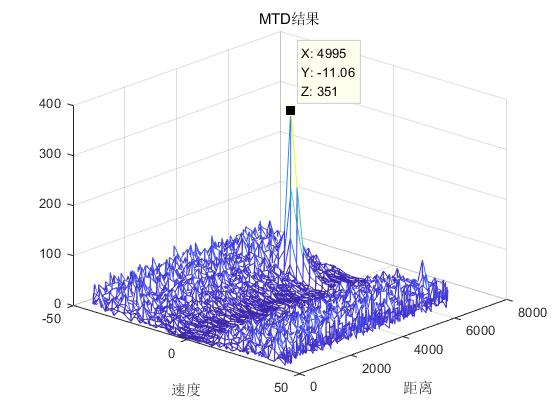
相参积累

1
2
3
4
5
6
7
8
9
10
11
12
13
%% 相参积累

for l = 1:1:length(PC_data(1,:))
    PC_data_CA(:,l) =fftshift( fft(PC_data(:,l)));  %对每一列FFT（相参积累）
end

figure
x =(1:length(PC_data_CA(1,:))) *c/10e6/2;
y = (-round( length(PC_data_CA(:,1))/2  ):1:round( length(PC_data_CA(:,1))/2 )-1 ) *lambda/( 2*T*length(PC_data_CA(:,1)) ); 
mesh(x,y ,abs(PC_data_CA));
title('相参处理结果');
xlabel('距离');ylabel('速度');
set(gca,'Ydir','reverse');

经过数字下变频，匹配滤波，相参处理后得到如下结果。

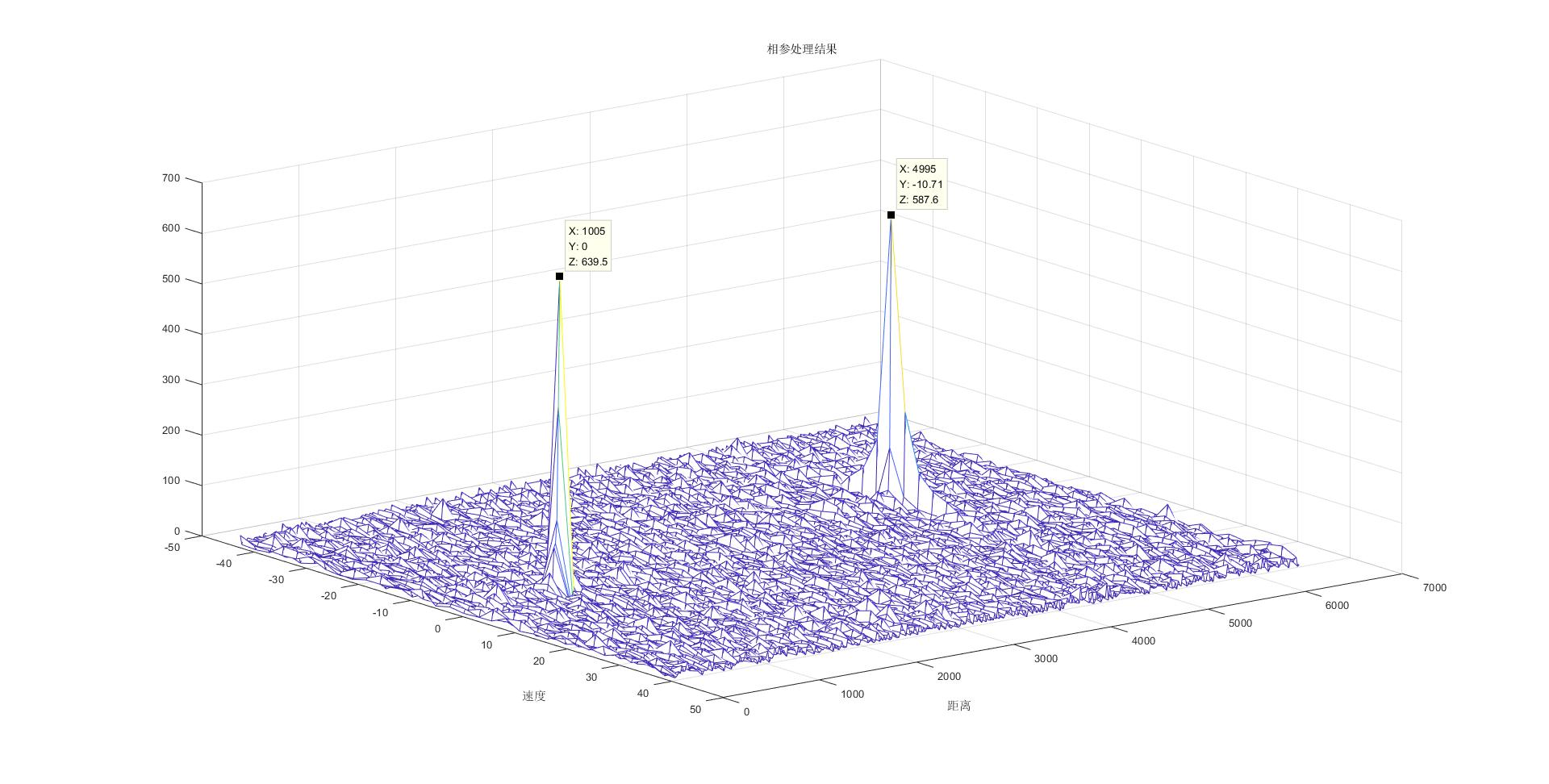
一个匹配滤波小实验

使用一单频连续波测速雷达，沿垂直其主瓣照射方向匀速推动，示意图如下：

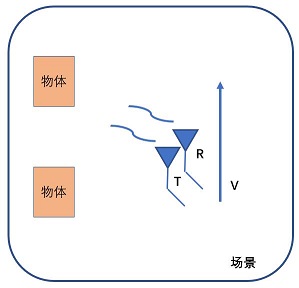
实际雷达照射面下的物体如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
IData =  csvread('Q6.csv');
QData =  csvread('I6.csv');

IData = IData(:,2);
QData = QData(:,2);

EchoData = QData + 1i*IData;
EchoData = EchoData(1:10:70000);
sizeEchoData = size(EchoData);
EchoData = reshape(EchoData,[1,sizeEchoData(1)]);

load('D:\Matlab2018a\SpeedDetect\GaussianWin_Point256_Alpha2_5.mat');
WinLength = length(GaussianWin_Point256_Alpha2_5);
Step = 20;
tEchoData = (1/25000 :1/25000 :7000*1/25000);
figure
subplot(2,1,1);
plot(tEchoData,real(EchoData));xlabel('时间（s）');ylabel('幅值（V）');title('时域波形（实）');
subplot(2,1,2);
plot(tEchoData,imag(EchoData));xlabel('时间（s）');ylabel('幅值（V）');title('时域波形（虚）');

result=STFT(EchoData,GaussianWin_Point256_Alpha2_5,WinLength,Step);

Fs = 2.5e3;
sizeResult = size(result);
t = 1/Fs*Step:1/Fs*Step:sizeResult(1)*1/Fs*Step;
v = -(WinLength-1)/2*Fs/WinLength/161 : Fs/WinLength/161 :  (WinLength-1)/2*Fs/WinLength/161;
figure
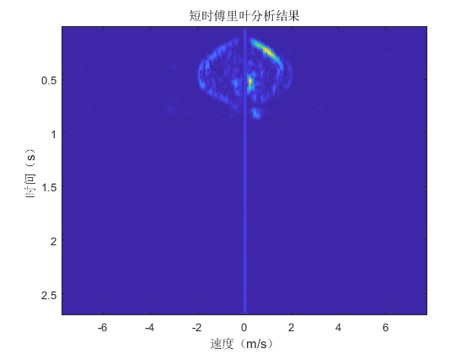
imagesc(v,t,abs(result));ylabel('时间（s）');xlabel('速度（m/s）');title('短时傅里叶分析结果');

Fs = 2.5e3;
angle_max = 10/360*2*pi;
h = 1.21;
d = tan(angle_max)*h;
va = 1.15;%2.34

t_total = d*2/va;
t = 0:1/Fs:t_total;

angle_now = atan( ( d*ones(1,length(t))- va*t)/h );
v_alpha = va * sin(angle_now);

fc = 24.15e9;
c = 3e8;

desire_signal = exp(1i*v_alpha*2*fc/c);
result = xcorr(EchoData,conj(desire_signal));
result = abs(result(6000:length(result)));

figure
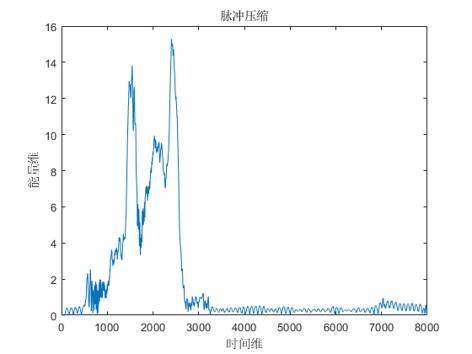
imagesc(abs(result));ylabel('能量维');xlabel('时间维');title('脉冲压缩');
figure
plot(abs(result));ylabel('能量维');xlabel('时间维');title('脉冲压缩');

实际回波的波形为

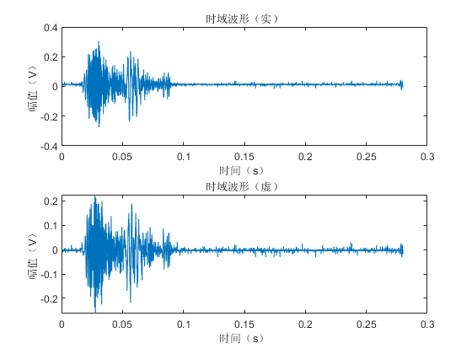
短时傅里叶分析结果为

脉冲压缩的结果为

连续波体制